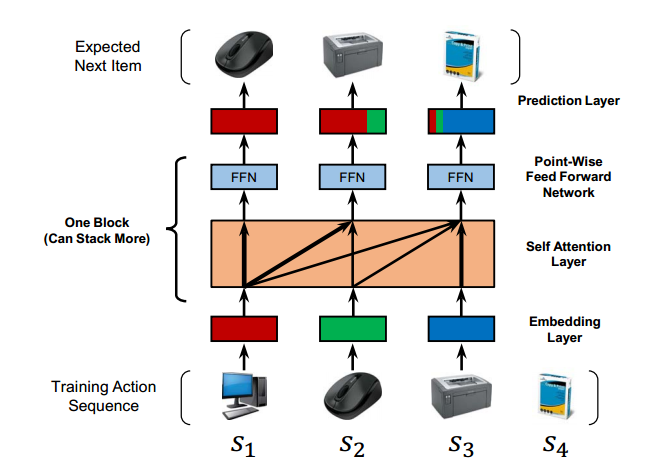
# Self-Attentive Sequential Recommendation

# 马尔科夫链（mc）

马尔科夫链（Markov Chain）是一种数学模型，用于描述一个系统从一个状态转移到另一个状态的过程。这种模型特别适用于分析随机过程，其中每个状态的转移仅依赖于当前状态，而与之前的状态无关。这种特性被称为 “马尔科夫性” 或 “无记忆性”。

# 基本概念

• 状态空间（State Space）: 马尔科夫链中的所有可能状态的集合。状态空间可以是有限的，也可以是无限的。
• 转移概率（Transition Probability）: 从一个状态转移到另一个状态的概率，通常表示为 $P (X_{n+1}=j\mid X_{n}=i) $,其中$ X_n$表示在时间$ n$ 的状态
• 转移矩阵（Transition Matrix）: 描述所有状态之间的转移概率的矩阵。对于一个有限状态空间的马尔科夫链，转移矩阵$P$ 的每个元素$P_{ij}$ 表示从状态$i$ 转移到状态$j$ 的概率
• 初始分布（Initial Distribution）: 系统在初始时刻的状态分布，通常表示为一个向量。

# 类型

• 离散时间马尔科夫链（DTMC）: 时间步长是离散的，每个时间步系统转移一次。
• 连续时间马尔科夫链（CTMC）: 时间是连续的，系统可以在任意时刻发生状态转移。

# 马尔科夫链的性质

1. 稳态分布（Steady-State Distribution）: 在长期运行中，马尔科夫链可能会达到一个稳定的状态分布，即各状态的概率不再随时间变化。这种分布可以通过求解$\pi P=\pi$ 来获得，其中$\pi$ 是稳态概率向量。

2. 回归性（Recurrence）: 如果一个状态从任意其他状态出发，总有一定的概率返回到该状态，则称这个状态是回归的。反之，如果返回概率为零，则称为瞬时的。

3. 不可约性（Irreducibility）: 如果系统的任意两个状态之间都可以通过若干步转移相互到达，则称这个马尔科夫链是不可约的。

4. 周期性（Periodicity）: 一个状态的周期定义为从该状态回到自身所需步数的最大公约数。如果这个周期为 1，则称该状态是非周期的。

5. 稳态概率向量（Steady-State Probability Vector），记作 $\pi$，是马尔科夫链中一个重要的概念。它描述了在长期运行中，系统各个状态的概率分布。当一个马尔科夫链达到稳态时，各个状态的概率将不再随时间变化。具体来说，如果一个马尔科夫链在某一时刻达到了稳态，那么无论经过多少次状态转移，系统各状态的概率将保持不变。

   • 不变形：$\pi P=\pi$ , 这里的$\pi$ 是一个行向量，表示各状态的稳态概率，P 是转移矩阵，描述各状态之间的转移概率。

   • 归一化条件：$\sum_i\pi_i=1$ 即稳态概率向量的各个元素之和为 1，表示系统必定处于某个状态。

   • 求解方法：要找到马尔科夫链的稳态概率向量 $\pi$，通常需要解以下线性方程组：

     $$\begin{cases}\pi P=\pi\\\sum_i\pi_i=1\end{cases}$$

# 一阶马尔科夫链

• 一阶马尔可夫链假设系统的下一个状态只依赖于当前状态。这在序列推荐系统中意味着，用户的下一次操作只取决于他们的最近一次操作。
• ** 状态表示：** 将用户的每一个操作视为一个状态。例如，用户购买的商品或浏览的网页。
• ** 转移概率矩阵：** 创建一个矩阵，表示从一个状态转移到另一个状态的概率。矩阵中的每个元素$P_{ij}$ 表示从状态$i$ 转移到状态$j$ 的概率。
• 概率计算：通过统计历史数据，计算从每个状态转移到其他状态的频率。例如，如果用户最近购买了商品 A，那么我们统计他们接下来购买商品 B 的频率来估计转移概率。
• 预测下一状态：根据当前状态（用户的最近一次操作），利用转移概率矩阵预测用户的下一次操作。例如，如果当前状态是商品 A，查看矩阵中与商品 A 对应的行，选择转移概率最高的商品作为预测结果。

# 高阶马尔科夫链

• ** 功能：** 将用户的每一个操作视为一个状态，并将一系列连续的操作视为一个组合状态。例如，用户最近连续购买了商品 A、B 和 C，这个组合状态可以表示为 (A, B, C)。高阶马尔可夫链假设系统的下一个状态不仅依赖于当前状态，还依赖于前几个状态。这在序列推荐系统中意味着，用户的下一次操作取决于他们的多个最近操作。
• 状态表示：将用户的每一个操作视为一个状态，并将一系列连续的操作视为一个组合状态。例如，用户最近连续购买了商品 A、B 和 C，这个组合状态可以表示为 (A, B, C)。
• 转移概率矩阵：创建一个更复杂的转移概率矩阵，表示从一个组合状态转移到下一个状态的概率。矩阵中的每个元素$P_{ijk}$ 表示从状态组合$(i,j)$ 转移到状态$k$ 的概率
• 概率计算：通过统计历史数据，计算从每个组合状态转移到其他状态的频率。例如，如果用户最近购买了商品 A 和 B，那么我们统计他们接下来购买商品 C 的频率来估计转移概率。
• 预测下一状态：根据当前组合状态（用户的最近几次操作），利用转移概率矩阵预测用户的下一次操作。例如，如果当前组合状态是 (A, B)，查看矩阵中与 (A, B) 对应的行，选择转移概率最高的商品作为预测结果。

# 递归神经网络（Recurrent Neural Network, RNN）

递归神经网络（Recurrent Neural Network, RNN）是一类用于处理序列数据的神经网络。与传统的前馈神经网络不同，RNN 具有记忆能力，可以处理和分析时间序列数据，捕捉数据中的时间依赖关系和顺序信息。RNN 在自然语言处理、语音识别、时间序列预测等领域有广泛的应用。

# 基本结构

RNN 的基本结构包括输入层、隐藏层和输出层。与传统神经网络不同的是，RNN 的隐藏层不仅接收当前时间步的输入，还接收前一个时间步的隐藏状态。具体来说：

• 输入层：接收序列数据的当前时间步输入$x_t$。

• 隐藏层：计算当前时间步的隐藏状态$h_t$，同时考虑当前输入$x_t$ 和前一个时间步的隐藏状态 $ h_{t-1}$

• 输出层：根据当前隐藏状态$h_t$ 计算输出$y_t$

• 隐藏状态的更新公式如下：

  $$h_t=\sigma(W_{xh}x_t+W_{hh}h_{t-1}+b_h)$$

  其中，$W_{xh}$ 和$W_{hh}$ 是权重矩阵，$b_n$ 是偏置向量，$\sigma$ 是激活函数（如 tanh 或 ReLU）

# 优势

1. 捕捉时间依赖：RNN 能够处理序列数据，捕捉其中的时间依赖关系，使其在处理时间序列数据和自然语言处理任务中表现良好。
2. 参数共享：RNN 的权重在每个时间步共享，减少了模型参数的数量，使其在处理长序列数据时更加高效。

# 局限性

1. 梯度消失和梯度爆炸：在处理长序列数据时，RNN 可能会遇到梯度消失或梯度爆炸的问题，使得模型难以训练。
2. 长时间依赖捕捉困难：标准 RNN 在处理长时间依赖关系时表现不佳。

# 顺序推荐

# 目标

将用户行为的个性化模型（基于历史活动）与用户最近行为的 “上下文” 概念结合起来进行推荐。

# 前人方式

• 马尔科夫链假设下一个动作仅由以前一个动作（或前几个动作）为条件，并已成功地用于表征推荐的短距离项目转换。

• 递归神经网络 RNN：RNN 是一种用于处理序列数据的神经网络，具有记忆能力，可以捕捉序列数据中的时间依赖关系。RNN 的基本结构包括输入层、隐藏层和输出层，其中隐藏层的状态会根据前一个时间步的隐藏状态和当前时间步的输入来更新

# Transformer

# 介绍

Transformer 是一种用于处理序列数据的深度学习模型，特别擅长于自然语言处理任务，如机器翻译、文本生成等。它由一个编码器（Encoder）和一个解码器（Decoder）组成。

# 编码器（Encoder）

编码器的任务是接收输入序列（例如，一个句子），并将其转换为一组特征表示。编码器包含多个层，每层都有两个主要部分：

1. 自注意力层（Self-Attention Layer）：用于计算每个词与其他词的相关性。
2. 前馈神经网络层（Feed-Forward Neural Network）：对自注意力层的输出进行进一步处理。

每一层都有一个 “残差连接”（Residual Connection）和 “层归一化”（Layer Normalization）来帮助训练更深的网络。

# 解码器（Decoder）

解码器的任务是根据编码器的输出生成目标序列（例如，翻译后的句子）。解码器也包含多个层，每层与编码器类似，但增加了一个 “编码器 - 解码器注意力层”（Encoder-Decoder Attention Layer），用来关注编码器的输出。

# 残差连接（Residual Connection）

# 原理

残差连接是一种深度神经网络的技术，通过在每个层之间引入直接的跳跃连接来帮助训练更深层的网络。具体来说，残差连接将输入直接添加到输出上，即：

$$\mathbf{y}=\mathcal{F}(\mathbf{x})+\mathbf{x}$$

其中，$\mathbf{x}$ 是输入，$\mathcal{F}(\mathbf{x})$ 是一个或多个层的非线性变换，$\mathbf{y}$ 是输出。

# 优点

1. 解决梯度消失问题：在深层网络中，梯度可能会在传播过程中逐渐消失，使得前面的层无法得到有效更新。残差连接通过直接传递梯度，缓解了这个问题。
2. 加速训练：残差连接提供了一条无需学习的捷径，使得网络更容易学习到有效的表示，从而加速训练过程。
3. 提高准确性：在很多应用中，使用残差连接的网络（如 ResNet）在准确性上有显著提升。

# 应用

残差连接最初在 ResNet（残差网络）中得到应用，后来在 Transformer 等模型中广泛使用，成为深度学习模型中的标准组件。

# 自注意力机制（Self-Attention）

自注意力机制是 Transformer 的核心。它的作用是让模型能够 “关注” 输入序列中不同位置的词之间的关系。这是如何做到的：

1. 输入嵌入（Input Embeddings）：
   • 首先，将输入序列中的每个词转换为一个高维向量（嵌入向量）。
2. 生成查询（Query）、键（Key）和值（Value）向量：
   • 对每个输入词的嵌入向量，通过不同的线性变换，生成对应的查询、键和值向量。
3. 计算注意力得分（Attention Scores）：
   • 对每个词的查询向量和所有词的键向量进行点积运算，得到注意力得分。这个得分表示当前词与其他词的相关性。
4. 归一化注意力得分：
   • 使用 Softmax 函数对注意力得分进行归一化，得到每个词的注意力权重。
5. 计算加权和：
   • 使用这些注意力权重对所有词的值向量进行加权求和，得到当前词的新的表示。
6. 允许每个词根据其与其他词的相关性进行加权求和，从而捕捉到全局信息。

# SASRec

# 培训简化图

# 要点

• 自我注意：发现句子中单词之间的句法和语意模式
• 可以并行加速

# 符号表

# 嵌入层

我们现将序列$(S^u_1, S^u_2, ..., S^u _{|S^{u-1}|})$ 变换为固定长度的序列$s=(s_1,s_2,...,s_n)$，其中 n 表示模型可以处理的最大长度，如果序列长度大于 n 则考虑最近的 n 个动作，如果序列长度小于 n，则在左边重复添加一个 ' 填充 ' 项，直到长度为 N 为止 0。其创建了一个项目嵌入矩阵$\mathbf{M} \in \mathbb{R}^{ |I| \times d}$，其中 d 是潜在维数，检索输入嵌入矩阵。

# 自注意力缩放点积注意力计算过程

$$\text{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\text{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}}\right)\mathbf{V}$$

# 解释

• Q：查询矩阵
• K：键矩阵
• V：值矩阵
• 点积计算：首先查询矩阵 Q 和建矩阵 K 的转置$K^T$ 的点积。这个点积结果表示查询和键之间的相似度
• 缩放：由于点积的结果在维度较大时可能会产生很大的数值，因此我们需要将点积结果除以$\sqrt d$ 进行缩放，其中$d$ 是键向量的维度。这样做的目的是为了避免在计算 softmax 时数值较大，导致梯度消失问题。
• softmax：通过 softmax 函数将缩放后的点积结果转换为概率分布。softmax 的作用是将每个查询与所有键的相似度转化为权重，这些权重表示每个键对当前查询的重要性。
• 加权求和：最后，将这些权重与值矩阵 V 相乘，得到最终的注意力输出。这一步的目的是根据查询对键的注意力权重，对值进行加权求和，从而得到每个查询对应的加权值。

# softmax 函数

$$\mathrm{softmax}(z_i)=\frac{e^{z_i}}{\sum_{j=1}^Ke^{z_j}}$$

其中，$z_i$ 是输入向量中的第 $i $ 个元素， $K$ 是向量的维度。

# 自注意层

• 旧方法：使用相同的对象作为查询、键和值。

• 该论文方法：将嵌入的 E 作为输入，通过线性投影将其转换为三个矩阵，并且发送到注意层中。

  $$\mathbf{S}=\mathrm{SA}(\widehat{\mathbf{E}})=\mathrm{Attention}(\widehat{\mathbf{E}}\mathbf{W}^Q,\widehat{\mathbf{E}}\mathbf{W}^K,\widehat{\mathbf{E}}\mathbf{W}^V),$$

• 投影矩阵$\mathbf{W}^Q,\mathbf{W}^K,\mathbf{W}^V\in\mathbb{R}^{d\times d}.$ 这些预测使得模型更灵活。

# 因果关系

模型在预测（t+1）-st 项时只考虑前 t 项，但是自注意层$S_t$ 的第$t$ 个输出包含后续项目的嵌入会让模型不稳定，所以我们通过进制$Q_i$ 和$K_j$$(j>i)$ 直接的所有联系来修改注意力。

# 点对点前馈网络

• 问题描述：虽然自注意力机制可以根据适应性权重聚合所有之前项目的嵌入，但其本质上仍然是线性模型。

• 解决方法：为了赋予模型非线性，并考虑不同潜在维度之间的交互，为每个 $S_i$ 应用一个点对点两层前馈网络，每个$S_i$ 的计算公式为：

  $$\mathbf{F}_i=\mathrm{FFN}(\mathbf{S}_i)=\mathrm{ReLU}(\mathbf{S}_i\mathbf{W}^{(1)}+\mathbf{b}^{(1)})\mathbf{W}^{(2)}+\mathbf{b}^{(2)}$$

  其中$W^{(1)}和W^{(2)}$ 是 d×d 矩阵，$b^{(1)}和b^{(2)}$ 是 d 维向量。并且$S_i$ 和$S_j$ 之间没有交互

  # FFN（前馈神经网络）

  FFN（Feed-Forward Neural Network，前馈神经网络）是神经网络的一种基本结构，通常用于对输入数据进行非线性变换。它由一个或多个全连接层（也称为密集层）组成，每个层都包含一组可学习的权重和偏置。

  # ReLU（线性修正单元）

  ReLU（Rectified Linear Unit，线性修正单元）是一种常用的激活函数。它的定义如下：

  $$\mathrm{ReLU}(x)=\max(0,x)$$

  ReLU 的作用是：

  1. 对于输入的每个元素，如果该元素小于 0，则输出 0。
  2. 如果该元素大于等于 0，则输出该元素本身。

# 堆叠自注意力块

• 问题描述：在第一个自注意力快后$F_i$ 本质上就聚合了所有之前项目的嵌入，$\text{(即}\hat{E}_{j},j\leq i)$, 但是我们可以以基于 F 的另一个自注意力块来学习更复杂的项目转换。

  $$\mathbf{S}^{(b)}=\mathbf{SA}(\mathbf{F}^{(b-1)})=\text{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}}\right)\mathbf{V},\\\mathbf{F}_{i}^{(b)}=\mathrm{FFN}(\mathbf{S}_{i}^{(b)}),\quad\forall i\in\{1,2,\ldots,n\},$$

  其中第一块定义为$S^{(1)}=S \ and \ F^{(1)}=F$

• 随着模型深入出现了一些问题，采取的措施为：

  $$g'(x)=x+\text{Dropout}(g(\text{LayerNorm}(x)))$$

  $$\begin{aligned} &1.\text{ 输入 }x: \\ &·x是上一层的输出或者当前层的输入。 \\ &\text{2. 层归一化(Layer Normalization):} \\ &\bullet\text{ 首先对输入 }x\text{ 进行层归一化:} \\ &\mathrm{LayerNorm}(x)=\frac{x-\mu}{\sqrt{\sigma^{2}+\epsilon}}\cdot\gamma+\beta \\ &\text{缩放和偏移参数。} \\ &\text{3. 应用函数 }g: \\ &· \\ &注意力机制(SA): \\ &g(\mathrm{LayerNorm}(x)) \\ &对于FFN,函数g的具体形式为: \\ &&&g(\mathrm{LayerNorm}(x))=\mathrm{ReLU}(\mathrm{LayerNorm}(x)\mathbf{W}^{(1)}+\mathbf{b}^{(1)})\mathbf{W}^{(2)}+\mathbf{b}^{(2)} \\ &\text{4.Dropout:} \\ &·&& \text{在应用函数 }g\text{ 之后,对结果应用Dropout,以防止过拟合:} \\ &&&\mathrm{Dropout}(g(\mathrm{LayerNorm}(x))) \\ &&&\text{Dropout的具体操作是在每次训练} \\ & \text{5. 残差连接(Residual Connection):} \\ &·&&& \text{最后,将Dropout的结果与原输入 }x\text{ 相加,实现残差连接}: \\ &&&g'(x)=x+\mathrm{Dropout}(g(\mathrm{LayerNorm}(x))) \end{aligned}$$

  其中 g (x) 表示自注意层或前馈网络。对于每层的 g，我们输入 g 之前都要对 x 进行层归一化，对 g 的输出应用 dropout，并将输入 x 添加到最终输出中。

# 层归一化

用于加速和稳定神经网络的训练过程。它通过在每一层对输入进行归一化，解决了在深层神经网络中训练时可能遇到的一些问题，例如梯度消失和梯度爆炸。

层归一化的基本思想是对每个神经元的输入进行归一化，使得输入的均值为 0，方差为 1。与批量归一化（Batch Normalization）不同，层归一化在计算归一化统计量时，只考虑当前层的输入，而不是一个小批量的数据。

$$\mathrm{LayerNorm}(\mathbf{x})=\alpha\odot\frac{\mathbf{x}-\mu}{\sqrt{\sigma^{2}+\epsilon}}+\beta,$$

其中$\odot$ 是元素向乘积，是指对两个相同维度的矩阵或向量进行对应元素的逐个相乘。这个操作不同于矩阵乘法，它不涉及矩阵之间的行列相乘和求和，只是简单地对对应位置的元素进行乘积运算。

# 元素向量积的数学表示

假设有两个相同维度矩阵 A 和 B，元素分别为$A_{ij}$ 和$B_{ij}$，则它们的元素向量积 C 可以表示为：

$$\begin{aligned}&C=A\odot B\\\\&\text{其中,}C_{ij}=A_{ij}\times B_{ij}。\end{aligned}$$

# 举个例子

$$\begin{aligned} &假设有两个矩阵A和B: \\ &A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix} \\ &B=\begin{pmatrix}7&8&9\\10&11&12\end{pmatrix} \\ &\text{它们的元素向乘积 C 为:} \\ &C=A\odot B=\begin{pmatrix}1\times7&2\times8&3\times9\\4\times10&5\times11&6\times12\end{pmatrix}=\begin{pmatrix}7&16&27\\40&55&72\end{pmatrix} \end{aligned}$$

# 预测层

在 b 个自我关注快后根据$F_{t}^{(b)}$ 来预测下一个项目。具体来说采用 MF 层来预测项目$i$ 的相关性。

• MF 层（Matrix Factorization Layer，矩阵分解层）在推荐系统中是指一种使用矩阵分解技术来预测用户与物品之间的交互评分或相关性的方法。矩阵分解是一种常见的协同过滤技术，通过将用户 - 物品评分矩阵分解为两个低维矩阵来建模用户偏好和物品特征

• 矩阵分解的目标是将一个大矩阵分解为两个更小的矩阵，这两个矩阵的乘积近似于原始矩阵。在推荐系统中，通常有一个用户 - 物品评分矩阵 R，其中$R_{ij}$ 表示用户 i 对物品 j 的评分。矩阵分解的目的是将 R 分解为两个地位矩阵 U 和 V。

• $$\begin{aligned}&R\approx UV^T\\&\text{其中:}\\&\bullet\quad U\text{ 是用户矩阵,维度为 }m\times k\text{,每一行对应一个用户的隐向量表示。}\\&\bullet\quad V\text{ 是物品矩阵,维度为 }n\times k\text{,每一行对应一个物品的隐向量表示。}\\&\bullet\quad k\text{ 是隐向量的维度,也称为潜在特征的数量。}\end{aligned}$$

$$r_{i,t}=\mathbf{F}_t^{(b)}\mathbf{N}_i^T,$$

• $r_{i,t}$ 是物品 i 在时间步 t 被推荐的相关性分数。
• $F_t $ 是用户在时间步 t 的隐向量表示。
• $N_i$ 是物品 i 的隐向量表示。

在这里我们使用单项嵌入 M 的方案，即

$$r_{i,t}=\mathbf{F}_{t}^{(b)}\mathbf{M}_{i}^{T}$$

在此矩阵中嵌入矩阵 M 是一个大小为 | I|×d 的矩阵，其中 | I | 是物品总数量，d 是嵌入向量的维度。

$F_{t}^{(b)}$ 可以表示为取决于项目嵌入 M 的函数，即：

$$\mathbf{F}_{t}^{(b)}=f(\mathbf{M}_{s_{1}},\mathbf{M}_{s_{2}},\ldots,\mathbf{M}_{s_{t}})$$

注意：需要实现不对称 ——$FFN(M_i)M_j^T≠FFN(M_j)M_i^T$

考虑用户之前的操作，并从访问过的项目的嵌入中得出隐式用户嵌入

# 网络层训练

我们将每个用户序列$(\mathcal{S}_{1}^{u},\mathcal{S}_{2}^{u},\ldots,\mathcal{S}_{|\mathcal{S}^{u}|-1}^{u})$ 转换为固定长度的序列$s=\{s_1,s_2,\ldots,s_n\}$：我们将$o_t$ 定义为时间步 t 的预期输出：

$$o_t=\begin{cases}\text{<pad>}&\text{如果 }s_t\text{是一个填充项}\\s_{t+1}&1\leq t<n\\S_{|S^u|}^u&t=n\end{cases}$$

• 其中 pad 表示填充项，我们的模型以序列$s$ 作为输入，响应的序列$o$ 为预期输出，我们采用二院交叉熵损失作为目标函数

  $$-\sum_{\mathcal{S}^u\in\mathcal{S}}\sum_{t\in[1,2,...,n]}\left[\log(\sigma(r_{o_t,t}))+\sum_{j\not\in\mathcal{S}^u}\log(1-\sigma(r_{j,t}))\right]$$

  $$\begin{aligned} &S:表示所有用户的集合。 \\ &S^{u}\colon\text{表示用户 }u\text{ 的序列。} \\ &t\colon\text{表示时间步,取值范围为 }\{1,2,\ldots,n\}。 \\ &o_{t}\colon\text{在时间步 }t\text{ 的预测输出。} \\ &r_{o_t,t}\text{:在时间步 }t\text{ 预测物品 }o_t\text{ 的相关性分数。} \\ &r_{j,t}\colon\text{ 在时间步 }t\text{ 预测物品 }j\text{ 的相关性分数,}j\notin S^u\text{ 表示不在用户 }u\text{ 的历史} \\ &\text{交互序列中的物品。} \\ &\sigma:表示sigmoid函数。 \end{aligned}$$

$$\begin{aligned}&\log(\sigma(r_{o_{t},t}))\text{:对于时间步 }t\text{ 的正样本 }o_t\text{,计算预测相关性分数的对数。}\\&\sum_{j\notin S^n}\log(1-\sigma(r_{j,t}))\text{:对于时间步 }t\text{ 的负样本集合,计算每个负样本}\\&\text{的预测相关性分数的对数。}\end{aligned}$$

$$\begin{aligned} &数,从而提高正样本的预测概率。 \\ &\text{负样本损失:通过}\sum_{j\notin S^{u}}\log(1-\sigma(r_{j,t})) \text{项,模型希望最小化负样本的预} \\ &\text{测相关性分数,从而降低负样本的预测概率。} \end{aligned}$$

# 讨论

• 因式分解马尔科夫链可得到：FMC 会对一阶项目转移矩阵进行因式分解，并根据上一项目$i$ 预测下一个项目$j$：

  $$P(j|i)\propto\mathbf{M}_i^T\mathbf{N}_j$$

  • $P(j|i)$ 表示在给定物品$i$ 的情况下，推荐物品$j$ 的概率
  • $M_i$ 表示物品$i$ 的嵌入向量
  • $N_j$ 表示物品$j$ 的嵌入向量
  • $M_i^j$ 表示物品$i$ 的嵌入向量$M_i$ 和物品$j$ 的嵌入向量$N_j$ 的内积

# 实验

# 问题

• SASRec 是否优于最先进的模型（包括基于 CNN/RNN 的方法）？
• SASRec 架构中各个组件的影响是什么？
• SASRec 的训练效率和可扩展性（关于 n）是多少？
• 注意力权重是否能够学习与位置或项目属性相关的有意义的模式？

# 数据集

• Amazon：[46] 中引入的一系列数据集，包含从 Amazon.com 抓取的大量产品评论语料库。Amazon 上的顶级产品类别被视为单独的数据集。我们考虑两个类别，“美容” 和 “游戏”。该数据集以其高稀疏性和多变性而著称。
• Steam：我们引入了一个从大型在线视频游戏分发平台 Steam 抓取的新数据集。该数据集包含 2,567,538 名用户、15,474 款游戏和 7,793,069 条英文评论，时间跨度为 2010 年 10 月至 2018 年 1 月。 该数据集还包含可能对未来工作有用的丰富信息，例如用户的游戏时间、定价信息、媒体评分、类别、开发者（等）
• MovieLens：一种广泛用于评估协同过滤算法的基准数据集。我们使用包含 100 万用户评分的版本（MovieLens-1M）。

将评论或评分的存在视为隐式反馈（即用户与商品进行了交互），并使用时间戳来确定操作的顺序。我们丢弃相关操作少于 5 个的用户和商品。为了进行分区，我们将每个用户 u 的历史序列 Su 分成三部分：

（1）用于测试的最近操作S^u_

（2）用于验证的第二最近操作S^u_

（3）用于训练的所有剩余操作。请注意，在测试期间，输入序列包含训练操作和验证操作

# 代码解析

# modules.py

这个代码实现了 Transformer 模型的一部分，主要包括位置编码、层归一化、嵌入、多头注意力机制和前馈神经网络。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

# -*- coding: utf-8 -*-
#/usr/bin/python2
'''
June 2017 by kyubyong park. 
kbpark.linguist@gmail.com.
https://www.github.com/kyubyong/transformer
'''

from __future__ import print_function
import tensorflow as tf
import numpy as np


def positional_encoding(dim, sentence_length, dtype=tf.float32):

    encoded_vec = np.array([pos/np.power(10000, 2*i/dim) for pos in range(sentence_length) for i in range(dim)])
    encoded_vec[::2] = np.sin(encoded_vec[::2])
    encoded_vec[1::2] = np.cos(encoded_vec[1::2])

    return tf.convert_to_tensor(encoded_vec.reshape([sentence_length, dim]), dtype=dtype)

def normalize(inputs, 
              epsilon = 1e-8,
              scope="ln",
              reuse=None):
    '''Applies layer normalization.
    
    Args:
      inputs: A tensor with 2 or more dimensions, where the first dimension has
        `batch_size`.
      epsilon: A floating number. A very small number for preventing ZeroDivision Error.
      scope: Optional scope for `variable_scope`.
      reuse: Boolean, whether to reuse the weights of a previous layer
        by the same name.
      
    Returns:
      A tensor with the same shape and data dtype as `inputs`.
    '''
    with tf.variable_scope(scope, reuse=reuse):
        inputs_shape = inputs.get_shape()
        params_shape = inputs_shape[-1:]
    
        mean, variance = tf.nn.moments(inputs, [-1], keep_dims=True)
        beta= tf.Variable(tf.zeros(params_shape))
        gamma = tf.Variable(tf.ones(params_shape))
        normalized = (inputs - mean) / ( (variance + epsilon) ** (.5) )
        outputs = gamma * normalized + beta
        
    return outputs

def embedding(inputs, 
              vocab_size, 
              num_units, 
              zero_pad=True, 
              scale=True,
              l2_reg=0.0,
              scope="embedding", 
              with_t=False,
              reuse=None):
    '''Embeds a given tensor.

    Args:
      inputs: A `Tensor` with type `int32` or `int64` containing the ids
         to be looked up in `lookup table`.
      vocab_size: An int. Vocabulary size.
      num_units: An int. Number of embedding hidden units.
      zero_pad: A boolean. If True, all the values of the fist row (id 0)
        should be constant zeros.
      scale: A boolean. If True. the outputs is multiplied by sqrt num_units.
      scope: Optional scope for `variable_scope`.
      reuse: Boolean, whether to reuse the weights of a previous layer
        by the same name.

    Returns:
      A `Tensor` with one more rank than inputs's. The last dimensionality
        should be `num_units`.
        
    For example,
    

inputs = tf.to_int32(tf.reshape(tf.range(2*3), (2, 3)))
outputs = embedding(inputs, 6, 2, zero_pad=True)
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(outputs)
>>
[[[ 0.          0.        ]
  [ 0.09754146  0.67385566]
  [ 0.37864095 -0.35689294]]

 [[-1.01329422 -1.09939694]
  [ 0.7521342   0.38203377]
  [-0.04973143 -0.06210355]]]
1
    

import tensorflow as tf

inputs = tf.to_int32(tf.reshape(tf.range(2*3), (2, 3)))
outputs = embedding(inputs, 6, 2, zero_pad=False)
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(outputs)
>>
[[[-0.19172323 -0.39159766]
  [-0.43212751 -0.66207761]
  [ 1.03452027 -0.26704335]]

 [[-0.11634696 -0.35983452]
  [ 0.50208133  0.53509563]
  [ 1.22204471 -0.96587461]]]    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
    '''
    with tf.variable_scope(scope, reuse=reuse):
        lookup_table = tf.get_variable('lookup_table',
                                       dtype=tf.float32,
                                       shape=[vocab_size, num_units],
                                       #initializer=tf.contrib.layers.xavier_initializer(),
                                       regularizer=tf.contrib.layers.l2_regularizer(l2_reg))
        if zero_pad:
            lookup_table = tf.concat((tf.zeros(shape=[1, num_units]),
                                      lookup_table[1:, :]), 0)
        outputs = tf.nn.embedding_lookup(lookup_table, inputs)
        
        if scale:
            outputs = outputs * (num_units ** 0.5) 
    if with_t: return outputs,lookup_table
    else: return outputs


def multihead_attention(queries, 
                        keys, 
                        num_units=None, 
                        num_heads=8, 
                        dropout_rate=0,
                        is_training=True,
                        causality=False,
                        scope="multihead_attention", 
                        reuse=None,
                        with_qk=False):
    '''Applies multihead attention.
    
    Args:
      queries: A 3d tensor with shape of [N, T_q, C_q].
      keys: A 3d tensor with shape of [N, T_k, C_k].
      num_units: A scalar. Attention size.
      dropout_rate: A floating point number.
      is_training: Boolean. Controller of mechanism for dropout.
      causality: Boolean. If true, units that reference the future are masked. 
      num_heads: An int. Number of heads.
      scope: Optional scope for `variable_scope`.
      reuse: Boolean, whether to reuse the weights of a previous layer
        by the same name.
        
    Returns
      A 3d tensor with shape of (N, T_q, C)  
    '''
    with tf.variable_scope(scope, reuse=reuse):
        # Set the fall back option for num_units
        if num_units is None:
            num_units = queries.get_shape().as_list[-1]
        
        # Linear projections
        # Q = tf.layers.dense(queries, num_units, activation=tf.nn.relu) # (N, T_q, C)
        # K = tf.layers.dense(keys, num_units, activation=tf.nn.relu) # (N, T_k, C)
        # V = tf.layers.dense(keys, num_units, activation=tf.nn.relu) # (N, T_k, C)
        Q = tf.layers.dense(queries, num_units, activation=None) # (N, T_q, C)
        K = tf.layers.dense(keys, num_units, activation=None) # (N, T_k, C)
        V = tf.layers.dense(keys, num_units, activation=None) # (N, T_k, C)
        
        # Split and concat
        Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0) # (h*N, T_q, C/h) 
        K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0) # (h*N, T_k, C/h) 
        V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0) # (h*N, T_k, C/h) 
    
        # Multiplication
        outputs = tf.matmul(Q_, tf.transpose(K_, [0, 2, 1])) # (h*N, T_q, T_k)
        
        # Scale
        outputs = outputs / (K_.get_shape().as_list()[-1] ** 0.5)
        
        # Key Masking
        key_masks = tf.sign(tf.reduce_sum(tf.abs(keys), axis=-1)) # (N, T_k)
        key_masks = tf.tile(key_masks, [num_heads, 1]) # (h*N, T_k)
        key_masks = tf.tile(tf.expand_dims(key_masks, 1), [1, tf.shape(queries)[1], 1]) # (h*N, T_q, T_k)
        
        paddings = tf.ones_like(outputs)*(-2**32+1)
        outputs = tf.where(tf.equal(key_masks, 0), paddings, outputs) # (h*N, T_q, T_k)
      
        # Causality = Future blinding
        if causality:
            diag_vals = tf.ones_like(outputs[0, :, :]) # (T_q, T_k)
            tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense() # (T_q, T_k)
            masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(outputs)[0], 1, 1]) # (h*N, T_q, T_k)
       
            paddings = tf.ones_like(masks)*(-2**32+1)
            outputs = tf.where(tf.equal(masks, 0), paddings, outputs) # (h*N, T_q, T_k)
      
        # Activation
        outputs = tf.nn.softmax(outputs) # (h*N, T_q, T_k)
         
        # Query Masking
        query_masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1)) # (N, T_q)
        query_masks = tf.tile(query_masks, [num_heads, 1]) # (h*N, T_q)
        query_masks = tf.tile(tf.expand_dims(query_masks, -1), [1, 1, tf.shape(keys)[1]]) # (h*N, T_q, T_k)
        outputs *= query_masks # broadcasting. (N, T_q, C)
          
        # Dropouts
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))
               
        # Weighted sum
        outputs = tf.matmul(outputs, V_) # ( h*N, T_q, C/h)
        
        # Restore shape
        outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2 ) # (N, T_q, C)
              
        # Residual connection
        outputs += queries
              
        # Normalize
        #outputs = normalize(outputs) # (N, T_q, C)
     
    if with_qk: return Q,K
    else: return outputs

def feedforward(inputs, 
                num_units=[2048, 512],
                scope="multihead_attention", 
                dropout_rate=0.2,
                is_training=True,
                reuse=None):
    '''Point-wise feed forward net.
    
    Args:
      inputs: A 3d tensor with shape of [N, T, C].
      num_units: A list of two integers.
      scope: Optional scope for `variable_scope`.
      reuse: Boolean, whether to reuse the weights of a previous layer
        by the same name.
        
    Returns:
      A 3d tensor with the same shape and dtype as inputs
    '''
    with tf.variable_scope(scope, reuse=reuse):
        # Inner layer
        params = {"inputs": inputs, "filters": num_units[0], "kernel_size": 1,
                  "activation": tf.nn.relu, "use_bias": True}
        outputs = tf.layers.conv1d(**params)
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))
        # Readout layer
        params = {"inputs": outputs, "filters": num_units[1], "kernel_size": 1,
                  "activation": None, "use_bias": True}
        outputs = tf.layers.conv1d(**params)
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))
        
        # Residual connection
        outputs += inputs
        
        # Normalize
        #outputs = normalize(outputs)
    
    return outputs

# 位置编码

1
2
3
4
5

def positional_encoding(dim, sentence_length, dtype=tf.float32):
    encoded_vec = np.array([pos/np.power(10000, 2*i/dim) for pos in range(sentence_length) for i in range(dim)])
    encoded_vec[::2] = np.sin(encoded_vec[::2])
    encoded_vec[1::2] = np.cos(encoded_vec[1::2])
    return tf.convert_to_tensor(encoded_vec.reshape([sentence_length, dim]), dtype=dtype)

• 定义了名为位置编码的函数， dim 表示向量的维度， sentence_length 表示句子的长度， dtype 表示输出张量的数据类型
• encoded_vec 使用嵌套列表解析生成一个 1D 的 numpy 数组 encoded_vec 。
  • 外层循环 for pos in range(sentence_length) 遍历句子的每个位置。
  • 内层循环 for i in range(dim) 遍历编码向量的每个维度。
  • 计算公式 pos/np.power(10000, 2*i/dim) 生成位置编码值。
• encoded_vec[::2] = np.sin(encoded_vec[::2]) : 这一行将编码向量中偶数索引位置的值替换为它们的正弦值，即 encoded_vec 的每隔两个元素（从索引 0 开始）的值。
• encoded_vec[1::2] = np.cos(encoded_vec[1::2]) : 这一行将编码向量中奇数索引位置的值替换为它们的余弦值，即 encoded_vec 的每隔两个元素（从索引 1 开始）的值。
• return : 行将 encoded_vec 重新调整为形状 [sentence_length, dim] ，即将其从 1D 数组重塑为 2D 数组。

# 层归一化

1
2
3
4
5
6
7
8
9
10
11
12
13

def normalize(inputs, 
              epsilon=1e-8,
              scope="ln",
              reuse=None):
    with tf.variable_scope(scope, reuse=reuse):
        inputs_shape = inputs.get_shape()
        params_shape = inputs_shape[-1:]
        mean, variance = tf.nn.moments(inputs, [-1], keep_dims=True)
        beta = tf.Variable(tf.zeros(params_shape))
        gamma = tf.Variable(tf.ones(params_shape))
        normalized = (inputs - mean) / ((variance + epsilon) ** 0.5)
        outputs = gamma * normalized + beta
    return outputs

# 函数作用域

• inputs : 输入张量
• epsilon : 一个小常数，用于避免除以零的情况，默认值为 1e-8 。
• scope : 变量作用域的名称，默认值为 "ln" 。
• reuse : 是否重用变量，默认值为 None 。

# 变量作用域

• scope : 变量作用域的名称。
• reuse : 是否重用现有的变量。

# 获取输入张量的形状

1
2

inputs_shape = inputs.get_shape()
params_shape = inputs_shape[-1:]

• inputs_shape : 获取输入张量的形状。
• params_shape : 获取最后一个维度的形状，这将用于归一化参数 beta 和 gamma 的形状。

# 计算均值和方差

1

mean, variance = tf.nn.moments(inputs, [-1], keep_dims=True)

• tf.nn.moments(inputs, [-1], keep_dims=True) : 计算输入张量在最后一个维度上的均值和方差，并保持原始维度的形状。

# 定义变量

1
2

beta = tf.Variable(tf.zeros(params_shape))
gamma = tf.Variable(tf.ones(params_shape))

• beta : 偏移量变量，初始化为零，形状为 params_shape 。
• gamma : 缩放量变量，初始化为一，形状为 params_shape 。

# 归一化

1

normalized = (inputs - mean) / ((variance + epsilon) ** 0.5)

• 输入张量减去均值
• 然后除以标准差，添加 espsilon 是避免除以零

# 应用缩放和偏移

1

outputs = gamma * normalized + beta

• gamma * normalized : 对归一化后的张量进行缩放。
• gamma * normalized + beta : 对归一化并缩放后的张量进行偏移。

• 返回应用了层归一化后的输出张量 outputs 。

# 嵌入层

作用：将输入的词 ID 映射到对应的嵌入向量。通过嵌入表查找，生成词嵌入矩阵，可以选择是否将 ID 为 0 的词嵌入设为 0，且可以对嵌入进行缩放。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def embedding(inputs, 
              vocab_size, 
              num_units, 
              zero_pad=True, 
              scale=True,
              l2_reg=0.0,
              scope="embedding", 
              with_t=False,
              reuse=None):
    with tf.variable_scope(scope, reuse=reuse):
        lookup_table = tf.get_variable('lookup_table',
                                       dtype=tf.float32,
                                       shape=[vocab_size, num_units],
                                       regularizer=tf.contrib.layers.l2_regularizer(l2_reg))
        if zero_pad:
            lookup_table = tf.concat((tf.zeros(shape=[1, num_units]),
                                      lookup_table[1:, :]), 0)
        outputs = tf.nn.embedding_lookup(lookup_table, inputs)
        
        if scale:
            outputs = outputs * (num_units ** 0.5) 
    if with_t: return outputs, lookup_table
    else: return outputs

# 定义函数

1
2
3
4
5
6
7
8
9

def embedding(inputs, 
              vocab_size, 
              num_units, 
              zero_pad=True, 
              scale=True,
              l2_reg=0.0,
              scope="embedding", 
              with_t=False,
              reuse=None):

• inputs : 输入张量，通常是词汇的索引。
• vocab_size : 词汇表的大小，即词汇的数量。
• num_units : 嵌入向量的维度，即每个词汇映射后的向量表示的长度。
• zero_pad : 是否将索引为 0 的位置填充为零向量，默认为 True 。
• scale : 是否对嵌入向量进行缩放，默认为 True 。
• l2_reg : L2 正则化的参数，默认为 0.0 。
• scope : 变量作用域的名称，默认为 "embedding" 。
• with_t : 是否返回嵌入矩阵，默认为 False 。
• reuse : 是否重用变量，默认为 None 。

# 变量作用域

1

with tf.variable_scope(scope, reuse=reuse):

• scope : 变量作用域的名称。
• reuse : 是否重用现有的变量。

# 创建嵌入矩阵

1
2
3
4

lookup_table = tf.get_variable('lookup_table',
                               dtype=tf.float32,
                               shape=[vocab_size, num_units],
                               regularizer=tf.contrib.layers.l2_regularizer(l2_reg))

• lookup_table : 创建嵌入矩阵变量，形状为 [vocab_size, num_units] 。意味着你有 vocab_size 个单词，每个单词都被表示为一个 num_units 维的向量。
• dtype=tf.float32 : 数据类型为浮点数。
• regularizer=tf.contrib.layers.l2_regularizer(l2_reg) : 使用 L2 正则化。

# 填充零向量

1
2
3

if zero_pad:
    lookup_table = tf.concat((tf.zeros(shape=[1, num_units]),
                              lookup_table[1:, :]), 0)

• tf.zeros(shape=[1, num_units]) : 创建一个零向量，形状为 [1, num_units] 。
• tf.concat((tf.zeros(shape=[1, num_units]), lookup_table[1:, :]), 0) : 将零向量与嵌入矩阵的其余部分连接起来，从而使索引为 0 的位置填充为零向量。

# 查找嵌入矩阵

1

outputs = tf.nn.embedding_lookup(lookup_table, inputs)

• tf.nn.embedding_lookup(lookup_table, inputs) : 根据输入张量 inputs 中的索引查找嵌入矩阵 lookup_table 中的向量表示，并返回这些表示。

# 对嵌入向量进行缩放

1
2

if scale:
    outputs = outputs * (num_units ** 0.5) 

• outputs = outputs * (num_units ** 0.5) : 如果 scale 为 True ，则对嵌入向量进行缩放，缩放因子为 num_units 的平方根。

# 多头注意力机制 multihead_attention

作用：实现多头自注意力机制。将查询、键和值线性变换为多头形式，计算注意力权重并应用于值，通过多个头并行计算来捕捉不同的注意力模式，最后将输出拼接并添加残差连接.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

def multihead_attention(queries, 
                        keys, 
                        num_units=None, 
                        num_heads=8, 
                        dropout_rate=0,
                        is_training=True,
                        causality=False,
                        scope="multihead_attention", 
                        reuse=None,
                        with_qk=False):
    with tf.variable_scope(scope, reuse=reuse):
        if num_units is None:
            num_units = queries.get_shape().as_list[-1]
        
        Q = tf.layers.dense(queries, num_units, activation=None)
        K = tf.layers.dense(keys, num_units, activation=None)
        V = tf.layers.dense(keys, num_units, activation=None)
        
        Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0)
        K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0)
        V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0)

        outputs = tf.matmul(Q_, tf.transpose(K_, [0, 2, 1]))
        outputs = outputs / (K_.get_shape().as_list()[-1] ** 0.5)
        
        key_masks = tf.sign(tf.reduce_sum(tf.abs(keys), axis=-1))
        key_masks = tf.tile(key_masks, [num_heads, 1])
        key_masks = tf.tile(tf.expand_dims(key_masks, 1), [1, tf.shape(queries)[1], 1])
        
        paddings = tf.ones_like(outputs) * (-2**32 + 1)
        outputs = tf.where(tf.equal(key_masks, 0), paddings, outputs)
  
        if causality:
            diag_vals = tf.ones_like(outputs[0, :, :])
            tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense()
            masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(outputs)[0], 1, 1])
            paddings = tf.ones_like(masks) * (-2**32 + 1)
            outputs = tf.where(tf.equal(masks, 0), paddings, outputs)
  
        outputs = tf.nn.softmax(outputs)
         
        query_masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1))
        query_masks = tf.tile(query_masks, [num_heads, 1])
        query_masks = tf.tile(tf.expand_dims(query_masks, -1), [1, 1, tf.shape(keys)[1]])
        outputs *= query_masks
          
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))
        outputs = tf.matmul(outputs, V_)
        outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2)
        outputs += queries
    if with_qk: return Q, K
    else: return outputs

# 函数定义

1
2
3
4
5
6
7
8
9
10

def multihead_attention(queries, 
                        keys, 
                        num_units=None, 
                        num_heads=8, 
                        dropout_rate=0,
                        is_training=True,
                        causality=False,
                        scope="multihead_attention", 
                        reuse=None,
                        with_qk=False):

• queries : 查询张量。
• keys : 键张量。
• num_units : 注意力机制的维度，默认为 None 。
• num_heads : 注意力头的数量，默认为 8 。
• dropout_rate : Dropout 的概率，默认为 0 。
• is_training : 是否在训练模式，默认为 True 。
• causality : 是否应用因果掩码，默认为 False 。
• scope : 变量作用域的名称，默认为 "multihead_attention" 。
• reuse : 是否重用变量，默认为 None 。
• with_qk : 是否返回 Q 和 K 矩阵，默认为 False 。

# 变量作用域，设置 num_units

1

with tf.variable_scope(scope, reuse=reuse):

• 如果 num_units 为 None ，则将其设置为查询张量的最后一个维度。

# 线性变换

1
2
3

Q = tf.layers.dense(queries, num_units, activation=None)
K = tf.layers.dense(keys, num_units, activation=None)
V = tf.layers.dense(keys, num_units, activation=None)

• 对 queries 、 keys 和 values 进行线性变换，得到 Q 、 K 和 V 矩阵。

# 拆分和拼接

1
2
3

Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0)
K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0)
V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0)

tf.split(Q, num_heads, axis=2) ：

• 将 Q 矩阵沿着 axis=2 维度切分成 num_heads 个子矩阵。
• 假设 Q 的形状为 [batch_size, sequence_length, num_units] ，那么切分后的每个子矩阵的形状为 [batch_size, sequence_length, num_units / num_heads] 。

tf.concat(..., axis=0) ：

• 将上述切分得到的子矩阵在 axis=0 维度上拼接起来。
• 假设有 num_heads 个子矩阵，每个子矩阵的形状为 [batch_size, sequence_length, num_units / num_heads] ，那么拼接后的矩阵形状为 [batch_size * num_heads, sequence_length, num_units / num_heads] 。

# 计算注意力分数

1
2

outputs = tf.matmul(Q_, tf.transpose(K_, [0, 2, 1]))
outputs = outputs / (K_.get_shape().as_list()[-1] ** 0.5)

• Q_ ：形状为 [batch_size * num_heads, sequence_length, num_units / num_heads] 的查询矩阵。

  K_ ：形状为 [batch_size * num_heads, sequence_length, num_units / num_heads] 的键矩阵。

• 首先对 K_ 进行转置， tf.transpose(K_, [0, 2, 1])

• 然后使用 matmul 对矩阵进行点积

• 然后缩放点积注意力 K_.get_shape().as_list()[-1] ：得到 K_ 最后一个维度的大小，即 num_units / num_heads 。

• (K_.get_shape().as_list()[-1] ** 0.5) ：计算其平方根。

• 将 outputs 除以这个平方根，缩放点积的结果：

# 检验码

这段代码的目的是通过对 outputs （即点积注意力得分矩阵）进行掩码（masking）操作，以确保在计算注意力时，填充的位置（padding positions）不会对结果产生影响。让我们逐步分析每一行代码：

1
2
3
4
5
6

key_masks = tf.sign(tf.reduce_sum(tf.abs(keys), axis=-1))
key_masks = tf.tile(key_masks, [num_heads, 1])
key_masks = tf.tile(tf.expand_dims(key_masks, 1), [1, tf.shape(queries)[1], 1])

paddings = tf.ones_like(outputs) * (-2**32 + 1)
outputs = tf.where(tf.equal(key_masks, 0), paddings, outputs)

• tf.abs(keys) ：对 keys 的所有元素取绝对值。

• tf.reduce_sum(tf.abs(keys), axis=-1) ：对 keys 的最后一个维度（即特征维度）求和，结果是一个形状为 [batch_size, sequence_length] 的张量。

• tf.sign(...) ：对求和结果进行符号函数操作，非零值变为 1，零值保持为 0。这用于标记填充值（padding positions）。

• tf.tile(key_masks, [num_heads, 1]) ：复制 key_masks ，在第一个维度上复制 num_heads 次，以适应多头注意力的情况。结果形状为 [batch_size * num_heads, sequence_length] 。

• tf.expand_dims(key_masks, 1) ：在 key_masks 的第一个维度添加一个新的维度，结果形状为 [batch_size * num_heads, 1, sequence_length] 。

  tf.tile(..., [1, tf.shape(queries)[1], 1]) ：在新添加的维度上复制 tf.shape(queries)[1] 次，结果形状为 [batch_size * num_heads, sequence_length, sequence_length] 。

• tf.ones_like(outputs) ：创建一个与 outputs 形状相同的全 1 张量。

  * (-2**32 + 1) ：将全 1 张量的所有值乘以一个非常小的负数（近似于负无穷），这个值将用来替换填充位置的注意力得分，使这些位置的注意力得分在 softmax 计算时接近于 0。

• tf.equal(key_masks, 0) ：生成一个布尔张量，指示哪些位置是填充位置（ key_masks 为 0 的位置）。

  tf.where(...) ：根据布尔张量选择对应位置的值，如果为真，则选择 paddings 中的值，否则选择 outputs 中的值。这样，填充位置的注意力得分将被设置为一个非常小的负数。

# 因果掩码

1
2
3
4
5
6

if causality:
    diag_vals = tf.ones_like(outputs[0, :, :])
    tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense()
    masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(outputs)[0], 1, 1])
    paddings = tf.ones_like(masks) * (-2**32 + 1)
    outputs = tf.where(tf.equal(masks, 0), paddings, outputs)

如果 causality 为 True ，则应用因果掩码，以确保当前时间步之后的信息不会被访问。

创建下三角矩阵 tril 作为掩码，并将无效位置的分数设置为一个非常小的值（负无穷大）。

# 计算注意力权重

1

outputs = tf.nn.softmax(outputs)

• 对注意力分数应用 Softmax 函数，得到注意力权重。

# 查询掩码

1
2
3
4

query_masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1))
query_masks = tf.tile(query_masks, [num_heads, 1])
query_masks = tf.tile(tf.expand_dims(query_masks, -1), [1, 1, tf.shape(keys)[1]])
outputs *= query_masks

计算 query_masks ，用于掩码无效的查询。

对 query_masks 进行扩展和重复，使其适应多头注意力的形状。

将无效位置的权重设置为零。

# Dropout

1

outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))

• 对注意力权重应用 Dropout，以防止过拟合。

# 加权求和

1

outputs = tf.matmul(outputs, V_)

• 使用注意力权重对 V 进行加权求和，得到最终的输出。

# 拼接和残差连接

1
2

outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2)
outputs += queries

# 返回结果

1
2

if with_qk: return Q, K
else: return outputs

# 前馈神经网络 feedforward

# 函数定义

1
2
3
4
5
6

def feedforward(inputs, 
                num_units=[2048, 512],
                scope="multihead_attention", 
                dropout_rate=0.2,
                is_training=True,
                reuse=None)

• inputs : 输入张量。
• num_units : 列表，包含两个整数，分别表示第一个和第二个卷积层的输出维度，默认为 [2048, 512] 。
• scope : 变量作用域的名称，默认为 "multihead_attention" 。
• dropout_rate : Dropout 的概率，默认为 0.2 。
• is_training : 是否在训练模式，默认为 True 。
• reuse : 是否重用变量，默认为 None 。

# 变量作用域

1

with tf.variable_scope(scope, reuse=reuse):

# 第一个卷积层

1
2
3

params = {"inputs": inputs, "filters": num_units[0], "kernel_size": 1,
          "activation": tf.nn.relu, "use_bias": True}
outputs = tf.layers.conv1d(**params)

params : 一个包含第一个卷积层参数的字典。

• inputs : 输入张量。
• filters : 卷积层的输出维度，为 num_units[0] （2048）。
• kernel_size : 卷积核的大小，设置为 1 ，相当于全连接层。
• activation : 激活函数，使用 ReLU。
• use_bias : 是否使用偏置，设置为 True 。

outputs = tf.layers.conv1d(**params) : 应用 1D 卷积层。

# 第一次 Dropout

1

outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))

• 对第一个卷积层的输出应用 Dropout，以防止过拟合。
• rate=dropout_rate : Dropout 的概率。
• training=tf.convert_to_tensor(is_training) : 是否在训练模式。

# 第二个卷积层

1
2
3

params = {"inputs": outputs, "filters": num_units[1], "kernel_size": 1,
          "activation": None, "use_bias": True}
outputs = tf.layers.conv1d(**params)

• params : 一个包含第二个卷积层参数的字典。
  • inputs : 第一个卷积层的输出。
  • filters : 卷积层的输出维度，为 num_units[1] （512）。
  • kernel_size : 卷积核的大小，设置为 1 ，相当于全连接层。
  • activation : 激活函数，设置为 None （线性激活）。
  • use_bias : 是否使用偏置，设置为 True 。
• outputs = tf.layers.conv1d(**params) : 应用第二个 1D 卷积层。

# 第二次 Dropout

1

outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=tf.convert_to_tensor(is_training))

• 对第二个卷积层的输出应用 Dropout，以防止过拟合。
• rate=dropout_rate : Dropout 的概率。
• training=tf.convert_to_tensor(is_training) : 是否在训练模式。

# 残差连接

1

outputs += inputs

• 将原始的输入张量 inputs 加到当前的输出张量上，进行残差连接。这有助于缓解梯度消失问题，并允许梯度在深层网络中更好地传播。

# 返回结果

1

return outputs

• 返回最终的输出张量 outputs 。

这个函数实现了一个两层的前馈神经网络，每层之间应用 Dropout，并使用残差连接将输入直接添加到输出。这种结构在 Transformer 模型中非常常见，用于在每个时间步上独立地应用前馈神经网络，从而增强模型的表示能力。

Dropout 是一种用于防止神经网络过拟合的正则化技术。其核心思想是在每个训练步骤中随机地 “丢弃” 一部分神经元，即暂时忽略它们，并将它们的输出设置为零。这种做法强制神经网络在每次迭代中以不同的方式学习，从而降低对特定神经元或特定路径的依赖性，提高模型的泛化能力。

# model.py

这个代码实现了一个基于自注意力机制的推荐系统模型，主要包括以下几个部分：

1. 初始化方法：定义各种占位符和掩码。
2. 嵌入层：将输入序列嵌入到高维空间。
3. 位置编码：为每个位置添加位置编码。
4. Dropout：对嵌入序列进行 dropout。
5. 自注意力机制块：使用多头自注意力机制和前馈神经网络对序列进行建模。
6. 归一化：对序列进行归一化处理。
7. 正负样本嵌入和预测得分：计算正负样本的嵌入和预测得分。
8. 损失函数：计算二元交叉熵损失和正则化损失。
9. AUC 和优化器：定义 AUC 指标和优化器。
10. 预测函数：定义用于预测的函数。

这些部分共同构建了一个推荐系统模型，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

from modules import *


class Model():
    def __init__(self, usernum, itemnum, args, reuse=None):
        self.is_training = tf.placeholder(tf.bool, shape=())
        self.u = tf.placeholder(tf.int32, shape=(None))
        self.input_seq = tf.placeholder(tf.int32, shape=(None, args.maxlen))
        self.pos = tf.placeholder(tf.int32, shape=(None, args.maxlen))
        self.neg = tf.placeholder(tf.int32, shape=(None, args.maxlen))
        pos = self.pos
        neg = self.neg
        mask = tf.expand_dims(tf.to_float(tf.not_equal(self.input_seq, 0)), -1)

        with tf.variable_scope("SASRec", reuse=reuse):
            # sequence embedding, item embedding table
            self.seq, item_emb_table = embedding(self.input_seq,
                                                 vocab_size=itemnum + 1,
                                                 num_units=args.hidden_units,
                                                 zero_pad=True,
                                                 scale=True,
                                                 l2_reg=args.l2_emb,
                                                 scope="input_embeddings",
                                                 with_t=True,
                                                 reuse=reuse
                                                 )

            # Positional Encoding
            t, pos_emb_table = embedding(
                tf.tile(tf.expand_dims(tf.range(tf.shape(self.input_seq)[1]), 0), [tf.shape(self.input_seq)[0], 1]),
                vocab_size=args.maxlen,
                num_units=args.hidden_units,
                zero_pad=False,
                scale=False,
                l2_reg=args.l2_emb,
                scope="dec_pos",
                reuse=reuse,
                with_t=True
            )
            self.seq += t

            # Dropout
            self.seq = tf.layers.dropout(self.seq,
                                         rate=args.dropout_rate,
                                         training=tf.convert_to_tensor(self.is_training))
            self.seq *= mask

            # Build blocks

            for i in range(args.num_blocks):
                with tf.variable_scope("num_blocks_%d" % i):

                    # Self-attention
                    self.seq = multihead_attention(queries=normalize(self.seq),
                                                   keys=self.seq,
                                                   num_units=args.hidden_units,
                                                   num_heads=args.num_heads,
                                                   dropout_rate=args.dropout_rate,
                                                   is_training=self.is_training,
                                                   causality=True,
                                                   scope="self_attention")

                    # Feed forward
                    self.seq = feedforward(normalize(self.seq), num_units=[args.hidden_units, args.hidden_units],
                                           dropout_rate=args.dropout_rate, is_training=self.is_training)
                    self.seq *= mask

            self.seq = normalize(self.seq)

        pos = tf.reshape(pos, [tf.shape(self.input_seq)[0] * args.maxlen])
        neg = tf.reshape(neg, [tf.shape(self.input_seq)[0] * args.maxlen])
        pos_emb = tf.nn.embedding_lookup(item_emb_table, pos)
        neg_emb = tf.nn.embedding_lookup(item_emb_table, neg)
        seq_emb = tf.reshape(self.seq, [tf.shape(self.input_seq)[0] * args.maxlen, args.hidden_units])

        self.test_item = tf.placeholder(tf.int32, shape=(101))
        test_item_emb = tf.nn.embedding_lookup(item_emb_table, self.test_item)
        self.test_logits = tf.matmul(seq_emb, tf.transpose(test_item_emb))
        self.test_logits = tf.reshape(self.test_logits, [tf.shape(self.input_seq)[0], args.maxlen, 101])
        self.test_logits = self.test_logits[:, -1, :]

        # prediction layer
        self.pos_logits = tf.reduce_sum(pos_emb * seq_emb, -1)
        self.neg_logits = tf.reduce_sum(neg_emb * seq_emb, -1)

        # ignore padding items (0)
        istarget = tf.reshape(tf.to_float(tf.not_equal(pos, 0)), [tf.shape(self.input_seq)[0] * args.maxlen])
        self.loss = tf.reduce_sum(
            - tf.log(tf.sigmoid(self.pos_logits) + 1e-24) * istarget -
            tf.log(1 - tf.sigmoid(self.neg_logits) + 1e-24) * istarget
        ) / tf.reduce_sum(istarget)
        reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
        self.loss += sum(reg_losses)

        tf.summary.scalar('loss', self.loss)
        self.auc = tf.reduce_sum(
            ((tf.sign(self.pos_logits - self.neg_logits) + 1) / 2) * istarget
        ) / tf.reduce_sum(istarget)

        if reuse is None:
            tf.summary.scalar('auc', self.auc)
            self.global_step = tf.Variable(0, name='global_step', trainable=False)
            self.optimizer = tf.train.AdamOptimizer(learning_rate=args.lr, beta2=0.98)
            self.train_op = self.optimizer.minimize(self.loss, global_step=self.global_step)
        else:
            tf.summary.scalar('test_auc', self.auc)

        self.merged = tf.summary.merge_all()

    def predict(self, sess, u, seq, item_idx):
        return sess.run(self.test_logits,
                        {self.u: u, self.input_seq: seq, self.test_item: item_idx, self.is_training: False})

# 初始化方法 __init__

1
2
3
4
5
6
7
8
9

def __init__(self, usernum, itemnum, args, reuse=None):
    self.is_training = tf.placeholder(tf.bool, shape=())
    self.u = tf.placeholder(tf.int32, shape=(None))
    self.input_seq = tf.placeholder(tf.int32, shape=(None, args.maxlen))
    self.pos = tf.placeholder(tf.int32, shape=(None, args.maxlen))
    self.neg = tf.placeholder(tf.int32, shape=(None, args.maxlen))
    pos = self.pos
    neg = self.neg
    mask = tf.expand_dims(tf.to_float(tf.not_equal(self.input_seq, 0)), -1)

• 作用：定义一些占位符，用于接收输入数据。
  • self.is_training ：一个布尔型占位符，用于指示是否在训练模式。
  • self.u ：用户 ID 占位符。
  • self.input_seq ：输入序列的占位符。
  • self.pos 和 self.neg ：正样本和负样本的占位符。
  • mask ：掩码，用于掩盖输入序列中的填充值（0）。

# 变量域 "SASRec" 和嵌入层

1
2
3
4
5
6
7
8
9
10
11
12

with tf.variable_scope("SASRec", reuse=reuse):
    # sequence embedding, item embedding table
    self.seq, item_emb_table = embedding(self.input_seq,
                                         vocab_size=itemnum + 1,
                                         num_units=args.hidden_units,
                                         zero_pad=True,
                                         scale=True,
                                         l2_reg=args.l2_emb,
                                         scope="input_embeddings",
                                         with_t=True,
                                         reuse=reuse
                                         )

• 作用：将输入序列进行嵌入，生成嵌入矩阵和项目嵌入表。
  • embedding 函数：实现输入序列的嵌入，返回嵌入后的序列和嵌入表。

# 位置编码

1
2
3
4
5
6
7
8
9
10
11
12

t, pos_emb_table = embedding(
    tf.tile(tf.expand_dims(tf.range(tf.shape(self.input_seq)[1]), 0), [tf.shape(self.input_seq)[0], 1]),
    vocab_size=args.maxlen,
    num_units=args.hidden_units,
    zero_pad=False,
    scale=False,
    l2_reg=args.l2_emb,
    scope="dec_pos",
    reuse=reuse,
    with_t=True
)
self.seq += t

• 作用：对序列进行位置编码，添加位置信息到序列嵌入中。
  • embedding 函数：实现位置编码的嵌入，返回位置编码向量和位置嵌入表。

# Dropout

1
2
3
4

self.seq = tf.layers.dropout(self.seq,
                             rate=args.dropout_rate,
                             training=tf.convert_to_tensor(self.is_training))
self.seq *= mask

• 作用：对序列嵌入进行 dropout 操作，并应用掩码。

# 构建自注意力机制的块

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

for i in range(args.num_blocks):
    with tf.variable_scope("num_blocks_%d" % i):
        # Self-attention
        self.seq = multihead_attention(queries=normalize(self.seq),
                                       keys=self.seq,
                                       num_units=args.hidden_units,
                                       num_heads=args.num_heads,
                                       dropout_rate=args.dropout_rate,
                                       is_training=self.is_training,
                                       causality=True,
                                       scope="self_attention")

        # Feed forward
        self.seq = feedforward(normalize(self.seq), num_units=[args.hidden_units, args.hidden_units],
                               dropout_rate=args.dropout_rate, is_training=self.is_training)
        self.seq *= mask

• 作用：构建多个自注意力机制块，每个块包括自注意力层和前馈神经网络层。
  • multihead_attention 函数：实现多头自注意力机制。
  • feedforward 函数：实现前馈神经网络层。

# 归一化

1

self.seq = normalize(self.seq)

• 作用：对序列进行归一化处理。

# 计算正负样本的嵌入和预测得分

1
2
3
4
5
6
7
8
9
10
11

pos = tf.reshape(pos, [tf.shape(self.input_seq)[0] * args.maxlen])
neg = tf.reshape(neg, [tf.shape(self.input_seq)[0] * args.maxlen])
pos_emb = tf.nn.embedding_lookup(item_emb_table, pos)
neg_emb = tf.nn.embedding_lookup(item_emb_table, neg)
seq_emb = tf.reshape(self.seq, [tf.shape(self.input_seq)[0] * args.maxlen, args.hidden_units])

self.test_item = tf.placeholder(tf.int32, shape=(101))
test_item_emb = tf.nn.embedding_lookup(item_emb_table, self.test_item)
self.test_logits = tf.matmul(seq_emb, tf.transpose(test_item_emb))
self.test_logits = tf.reshape(self.test_logits, [tf.shape(self.input_seq)[0], args.maxlen, 101])
self.test_logits = self.test_logits[:, -1, :]

• 作用：计算正样本和负样本的嵌入，并通过矩阵乘法得到预测得分。

# 损失函数

1
2
3
4
5
6
7
8
9
10

self.pos_logits = tf.reduce_sum(pos_emb * seq_emb, -1)
self.neg_logits = tf.reduce_sum(neg_emb * seq_emb, -1)

istarget = tf.reshape(tf.to_float(tf.not_equal(pos, 0)), [tf.shape(self.input_seq)[0] * args.maxlen])
self.loss = tf.reduce_sum(
    - tf.log(tf.sigmoid(self.pos_logits) + 1e-24) * istarget -
    tf.log(1 - tf.sigmoid(self.neg_logits) + 1e-24) * istarget
) / tf.reduce_sum(istarget)
reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
self.loss += sum(reg_losses)

• 作用：计算模型的损失函数，包含正负样本的二元交叉熵损失和正则化损失。

# AUC 和优化器

1
2
3
4
5
6
7
8
9
10
11
12
13
14

tf.summary.scalar('loss', self.loss)
self.auc = tf.reduce_sum(
    ((tf.sign(self.pos_logits - self.neg_logits) + 1) / 2) * istarget
) / tf.reduce_sum(istarget)

if reuse is None:
    tf.summary.scalar('auc', self.auc)
    self.global_step = tf.Variable(0, name='global_step', trainable=False)
    self.optimizer = tf.train.AdamOptimizer(learning_rate=args.lr, beta2=0.98)
    self.train_op = self.optimizer.minimize(self.loss, global_step=self.global_step)
else:
    tf.summary.scalar('test_auc', self.auc)

self.merged = tf.summary.merge_all()

• 作用：定义 AUC 指标和优化器，如果 reuse 为 None 则初始化训练操作，否则记录测试 AUC。

# 预测函数 predict

1
2
3

def predict(self, sess, u, seq, item_idx):
    return sess.run(self.test_logits,
                    {self.u: u, self.input_seq: seq, self.test_item: item_idx, self.is_training: False})

• 作用：定义预测函数，接收会话、用户 ID、输入序列和项目索引，返回预测得分。

# util.py

这个代码包含了数据分割函数和模型评估函数，具体解析如下：

1. 数据分割函数 data_partition ：读取用户 - 物品交互数据，分割成训练集、验证集和测试集，并计算用户数和物品数。
2. 模型评估函数 evaluate ：在测试集上评估模型表现，计算 NDCG 和 HT。
3. 模型评估函数（验证集） evaluate_valid ：在验证集上评估模型表现，计算 NDCG 和 HT。

这些功能共同构成了一个基本的推荐系统数据处理和评估框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130

import sys
import copy
import random
import numpy as np
from collections import defaultdict


def data_partition(fname):
    usernum = 0
    itemnum = 0
    User = defaultdict(list)
    user_train = {}
    user_valid = {}
    user_test = {}
    # assume user/item index starting from 1
    f = open('data/%s.txt' % fname, 'r')
    for line in f:
        u, i = line.rstrip().split(' ')
        u = int(u)
        i = int(i)
        usernum = max(u, usernum)
        itemnum = max(i, itemnum)
        User[u].append(i)

    for user in User:
        nfeedback = len(User[user])
        if nfeedback < 3:
            user_train[user] = User[user]
            user_valid[user] = []
            user_test[user] = []
        else:
            user_train[user] = User[user][:-2]
            user_valid[user] = []
            user_valid[user].append(User[user][-2])
            user_test[user] = []
            user_test[user].append(User[user][-1])
    return [user_train, user_valid, user_test, usernum, itemnum]


def evaluate(model, dataset, args, sess):
    [train, valid, test, usernum, itemnum] = copy.deepcopy(dataset)

    NDCG = 0.0
    HT = 0.0
    valid_user = 0.0

    if usernum>10000:
        users = random.sample(xrange(1, usernum + 1), 10000)
    else:
        users = xrange(1, usernum + 1)
    for u in users:

        if len(train[u]) < 1 or len(test[u]) < 1: continue

        seq = np.zeros([args.maxlen], dtype=np.int32)
        idx = args.maxlen - 1
        seq[idx] = valid[u][0]
        idx -= 1
        for i in reversed(train[u]):
            seq[idx] = i
            idx -= 1
            if idx == -1: break
        rated = set(train[u])
        rated.add(0)
        item_idx = [test[u][0]]
        for _ in range(100):
            t = np.random.randint(1, itemnum + 1)
            while t in rated: t = np.random.randint(1, itemnum + 1)
            item_idx.append(t)

        predictions = -model.predict(sess, [u], [seq], item_idx)
        predictions = predictions[0]

        rank = predictions.argsort().argsort()[0]

        valid_user += 1

        if rank < 10:
            NDCG += 1 / np.log2(rank + 2)
            HT += 1
        if valid_user % 100 == 0:
            print '.',
            sys.stdout.flush()

    return NDCG / valid_user, HT / valid_user


def evaluate_valid(model, dataset, args, sess):
    [train, valid, test, usernum, itemnum] = copy.deepcopy(dataset)

    NDCG = 0.0
    valid_user = 0.0
    HT = 0.0
    if usernum>10000:
        users = random.sample(xrange(1, usernum + 1), 10000)
    else:
        users = xrange(1, usernum + 1)
    for u in users:
        if len(train[u]) < 1 or len(valid[u]) < 1: continue

        seq = np.zeros([args.maxlen], dtype=np.int32)
        idx = args.maxlen - 1
        for i in reversed(train[u]):
            seq[idx] = i
            idx -= 1
            if idx == -1: break

        rated = set(train[u])
        rated.add(0)
        item_idx = [valid[u][0]]
        for _ in range(100):
            t = np.random.randint(1, itemnum + 1)
            while t in rated: t = np.random.randint(1, itemnum + 1)
            item_idx.append(t)

        predictions = -model.predict(sess, [u], [seq], item_idx)
        predictions = predictions[0]

        rank = predictions.argsort().argsort()[0]

        valid_user += 1

        if rank < 10:
            NDCG += 1 / np.log2(rank + 2)
            HT += 1
        if valid_user % 100 == 0:
            print '.',
            sys.stdout.flush()

    return NDCG / valid_user, HT / valid_user

# 导入模块

1
2
3
4
5

import sys
import copy
import random
import numpy as np
from collections import defaultdict

作用：导入所需的模块，包括系统模块、深拷贝模块、随机数模块、数值计算模块和默认字典模块。

# 数据分割函数 data_partition

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30