Home Nature-Language-Process

# How do we represent the meaning of a word?

# Definition its meaning(Webster dictionary)

  • the idea that is represented by a word,phrase,etc
  • the idea that a person want to express by using words,signs,etc
  • the idea that is expressed in a work of writing,art,etc

# commonest linguistic way of thinking of meaning:

signifier(symbol)→signified(ideaorthing)signifier(symbol)→signified(idea or thing)

# problems with resources like WordNet

# Great as a resource but missing nuance

  • "proficient"is listed as a synonym for "good"——This is only correct in some contexts

# Missing new meanings of words

  • e.g.:"wicked,badass,nifty,wizard,genius,ninja,bombest"——Nearly impossible to keep up-to-date!

# Subjective

# Requires human labor to create and adapt

# Can't compute accurate word similarity

# Representing words as discrete symbols

# regard words as discrete symbols

  • hotel,conference,motel - these words respect as a localist representation

  • such symbols for words can be represented by one-hot vectors:

    motel=[000000000010000]hotel=[000000010000000]\text{motel}=[000000000010000]\\\text{hotel}=[000000010000000]

  • Vector dimension = number of words in vocabulary

# exiting problem

example :in web search,if user searches for "Seattle motel",we would like to match documents containing "Seattle hotel"

But:

motel=[000000000010000]hotel=[000000010000000]\text{motel}=[000000000010000]\\\text{hotel}=[000000010000000]

These two vectors are orthogonal (正交)

There is no natural notion of similarity for one-hot vectors!

# Solutions

  • Could try to rely on WordNet's list of synonyms to get similarity ?
    • But it is well-known to fail badly:incompleteness
  • **Instead :learn to encode similarity in the vectors themselves **

# Representing words by their context

# Distributional 分布语义学

EXTREMELY COMPUTATIONAL

  • A word's meaning is given by the word's that frequently appear close-by

  • "You shall know a word by the company it keeps" -----which is one of the most successfully ideas of modern statistical NLP!

  • When a word w appears in a text,its context is the set of words that appear nearby (within a fixed-size window)

  • Use the many contexts of w to build up a representation of w

    ...govemmentdebtproblemstumingintobanking‾crisesashappenedin2009......sayingthatEuropeneedsunifiedbanking‾regulationtoreplacethehodgepodge......Indiahasjustgivenitsbanking‾systemashotinthearm......govemment \ debt\ problem\ stuming\ into\ \underline{banking} \ crises \ as \ happened \ in \ 2009... \\ ...saying \ that \ Europe \ need \ sunified \ \underline{banking} \ regulation \ to \ replace \ the \ hodgepodge... \\ ...India \ has \ just \ given \ its \ \underline{banking} \ system \ a \ shot \ in \ the \ arm...

    • the context words will represent banking!

  • Find out a bunch of places where banking occurs in text,and will collect the sort of nearby words that context words.

  • When talking about a word in our natural language,we sort of have two senses of word which are referred to as types and tokens.

# Word vectors

build a vector for each word,chosen so that it is similar to vectors of words that appear in similar contexts.

banking=(0.2860.792−0.177−0.1070.109−0.5420.3490.271)banking =\quad\left(\begin{array}{c}0.286\\0.792\\-0.177\\-0.107\\0.109\\-0.542\\0.349\\0.271\end{array}\right)

Note: word vectors are also called word embeddings or (neural) word representations

# Word2vec

# Idea

  • We have a large corpus (语料) ("body") of text
  • Every word in a fixed vocabulary is represented by a vector
  • Go through each position t in the text,which has a center word c and context ("outside") words o
  • Use the similarity of the word vectors for c and o
  • Keep adjusting the word vectors to maximize this probability

# Overview

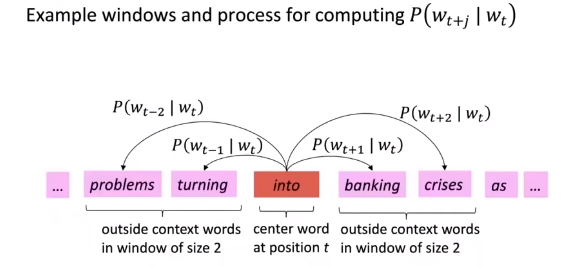
QQ_1722617653253.png

  • choose the center word into and analyze its context
  • If a model of predicting the probability of context words given the center word and this mode,we'll come to in a minute.
  • So,we need to find out what probability it gives to the words that actually occurred in the context of this word.

# problem

How can we work out the probability of a word occurring in the context of the center word?

# model

fixed: 固定的 likelihood: 可能性 variables: 变量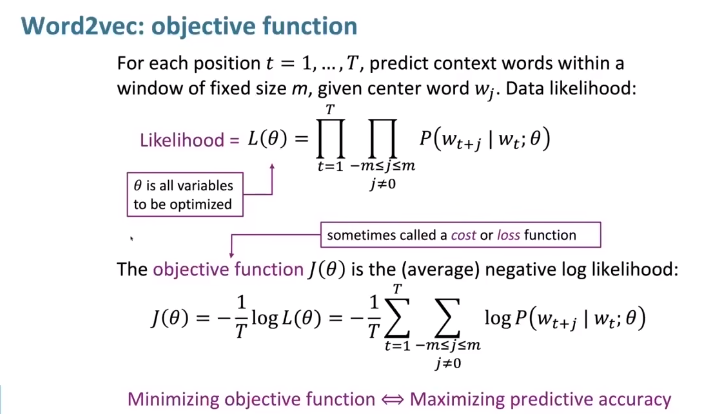
QQ_1722619161334.png

That's the setup,but how do we calculate the probability of a word occurring in the context?

QQ_1722619421863.png

The only thing we ought to do is to have vector representations for each word,and we're going to work out the probability simply in terms of the word vectors.

# prediction function

QQ_1722619629273.png

QQ_1722621298420.png

# Train the model

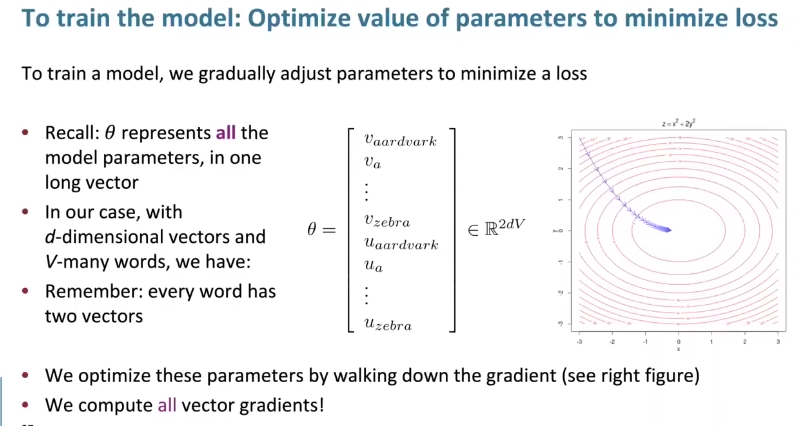
How to train the model?**We wanna to minimize our loss by fiddle our word vectors **.And maximize the probability of the words we actually saw in the context of the center word.

  • Remember! Each word have two vectors, its context vector and its center vector.
  • And below we put on the loss function

J(θ)=−1T∑t=1∑m≤j≤mlog⁡P(wt+j∣wt)J(\theta)=-\frac{1}{T}\sum_{t=1}\sum_{m\leq j\leq m}\log P(w_{t+j}|w_{t})

  • Following are the softmax function:

    p(o∣c)=exp⁡(uoTvc)∑w∈Vexp⁡(uwTvc)p(o|c)=\frac{\exp(u_{o}^{T}v_{c})}{\sum_{w \in V}\exp(u_{w}^{T}v_{c})}

  • And the partial derivative is :

    ∂∂vclog⁡exp⁡(uoTvc)∑w∈Vexp⁡(uwTvc)=∂∂vclog⁡exp⁡(uoTvc)−∂∂vclog⁡∑w∈VVexp⁡(uwTvc)\frac{\partial}{\partial v_{c}}\log\frac{\exp(u_{o}^{T}v_{c})}{\sum_{w\in V}\exp(u_{w}^{T}v_{c})} \\ =\frac{\partial}{\partial v_{c}}\log\exp(u_{o}^{T}v_{c})-\frac{\partial}{\partial v_{c}}\log\sum_{w \in V}^{V}\exp(u_{w}^{T}v_{c})