Home deep-learning
# 基础知识

# 损失函数（Loss Function）

# 定义：

损失函数用于量化模型预测值与真实值之间的差异。它是模型训练过程中需要最小化的目标函数。

# 常用损失函数及其数学表达式：

# 均方误差（Mean Squared Error,MSE）

常用于回归问题，计算预测值与真实值之间差的平方的平均值。

MSE=1N∑i=1N(yi−y^i)2MSE=\frac{1}{N}\sum_{i=1}^N(y_i-\hat{y}_i)^2

其中，yiy_i 是第ii 个样本的真实值，y^i\hat y_i 是第ii 个样本的预测值 ，NN 是样本总数。

# 交叉熵损失（Cross-Entropy Loss）

常用于分类问题，衡量预测概率分布与真实分布之间的差异

  • 对于二分类问题，交叉熵损失函数为：

    L=−1N∑i=1N[yilog⁡(y^i)+(1−yi)log⁡(1−y^i)]L=-\frac{1}{N}\sum_{i=1}^N[y_i\log(\hat{y}_i)+(1-y_i)\log(1-\hat{y}_i)]

  • 对于多分类问题，交叉熵损失函数为：

    L=−1N∑i=1N∑c=1Cyiclog⁡(y^ic)L=-\frac1N\sum_{i=1}^N\sum_{c=1}^Cy_{ic}\log(\hat y_{ic})

    其中，yicy_{ic} 表示第ii 个样本属于类别cc 的真实标签，y^ic\hat y_{ic} 表示第ii 个样本属于类别cc 的预测概率

# 绝对误差（Mean Absolute Error,MAE）

计算预测值与真实值之间差的绝对值的平均值。

MAE=1N∑i=1N∣yi−y^i∣MAE=\frac{1}{N}\sum_{i=1}^N|y_i-\hat{y}_i|

# 损失函数优化建议

损失函数的优化是通过优化算法（如梯度下降）不断调整模型参数，使损失函数值最小化的过程。以下是一些常见的优化建议：

# 梯度下降（Gradient Descent）

梯度下降是优化算法的一种，用于最小化损失函数。通过计算损失函数相对于参数的梯度，我们可以沿着梯度的反方向更新参数，从而逐步找到使损失函数最小的参数值。

梯度的定义：

df(x)dx=lim⁡h→0f(x+h)−f(x)h\frac{df(x)}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}h

这是导数的定义，表示函数f(x)f(x) 在点xx 处的瞬时变化率

数值梯度：

数值梯度使用上述定义，通过有限差分法来近似计算梯度：

df(x)dx≈f(x+h)−f(x)h\begin{aligned}\frac{df(x)}{dx}\approx\frac{f(x+h)-f(x)}{h}\end{aligned}

  • 标准梯度下降（Batch Gradient Descent）：使用整个训练集计算梯度更新参数。
  • 随机梯度下降（Stochastic Gradient Descent, SGD）：使用每个样本计算梯度更新参数。
  • 小批量梯度下降（Mini-Batch Gradient Descent）：使用小批量样本计算梯度更新参数。

# 自适应优化算法

  • AdaGrad：对每个参数使用自适应学习率，适合处理稀疏数据。
  • RMSProp：对梯度平方的移动平均值进行归一化，解决 AdaGrad 在非凸函数上收敛过慢的问题。
  • Adam：结合了 AdaGrad 和 RMSProp 的优点，对一阶矩和二阶矩的估计进行校正。

mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2m^t=mt1−β1tv^t=vt1−β2tθt+1=θt−αm^tv^t+ϵ\begin{aligned} &m_t=\beta_1m_{t-1}+(1-\beta_1)g_t \\ &v_t=\beta_2v_{t-1}+(1-\beta_2)g_t^2 \\ &\hat{m}_{t}=\frac{m_{t}}{1-\beta_{1}^{t}} \\ &\hat{v}_{t}=\frac{v_{t}}{1-\beta_{2}^{t}} \\ &\theta_{t+1}=\theta_{t}-\alpha\frac{\hat{m}_{t}}{\sqrt{\hat{v}_{t}}+\epsilon} \end{aligned}

​ 其中，gtg_t 是梯度，mtm_t 和vtv_t 分别是一阶和二阶矩估计，α\alpha 是学习率

# 评估指标

在模型评估过程中，除了损失函数，还需要使用各种评估指标来衡量模型性能。Recall 是分类任务中特别重要的指标之一。

# Recall（召回率）

召回率衡量的是模型在所有实际为正的样本中正确预测为正的比例。对于二分类问题，召回率的定义和数学表达式如下：

Recall=TPTP+FNRecall=\frac {TP}{TP+FN}

其中:

  • TP（Ture Positives）：真实为正的样本被正确预测为正
  • FN（False Negatives）：真实为正的样本被错误预测为负

召回率关注的是模型对正样本的识别能力，尤其在处理不平衡数据集（正样本较少）时，召回率是一个重要的评估指标。

# 准确率（Accuracy）:

Accuracy=TP+TNTP+TN+FP+FNAccuracy=\frac {TP+TN} {TP+TN+FP+FN}

其中：

  • TN（True Negatives）是真实为负的样本被正确预测为负
  • FP（False Positives）是真实为负的样本被错误预测为正。

# 精确率

precision=TPTP+FPprecision=\frac {TP}{TP+FP}

精确率衡量的是模型在所有被预测为正的样本中实际为正的比例。

# F1-score

精确率和召回率的调和平均数，综合考虑两者的平衡：

F1=2⋅Precision⋅RecallPrecision+RecallF1=2\cdot\frac{Precision\cdot Recall}{Precision+Recall}

# 支持向量积 (SVM) 损失函数及其优化

# 公式解释

# 得分函数：

s=f(x;W)=Wxs=f(x;W)=Wx

这里，ss 是输入xx 经过参数WW 的线性变换后的得分。

# SVM 损失函数

Li=∑j≠yimax⁡(0,sj−syi+1)L_i=\sum_{j≠y_i}\max(0,s_j-s_{y_i}+1)

这个公式计算了第 i 个样本的损失。对于第 i 个样本的每一个错误分类 j (即 j≠yi)，计算最大间隔损失max(0,sj−syi+1)max(0,s_j-s_{y_i}+1)，这意味着正确类的得分syis_{y_i} 比错误类的sjs_j 得分至少高一，则损失函数为 0，否则损失为sj−syi+1s_j-s_{y_i}+1

# 总损失

L=1N∑i=1NLi+∑kWk2L=\frac1N\sum_{i=1}^NL_i+\sum_kW_k^2

这里的总损失包含两个部分:

  • 数据损失：第一个部分1N∑i=1NLi{\frac{1}{N}}\sum_{i=1}^{N}L_{i} 是所有样本的平均损失
  • 正则化项：第二个部分∑kWk2\sum_kW_k^2 是权重WW 的 L2 正则化，用于防止过拟合

# 目标

want∇WL\mathrm{want}\quad\nabla_WL

这里的目标是计算损失函数LL 对参数WW 的梯度∇WL\quad\nabla_WL。这个梯度用于优化模型是参数，通过梯度下降或其他优化算法来最小化损失函数，从而提高模型性能。

# Convolutional Neural Network，CNN

# 神经网络图

123

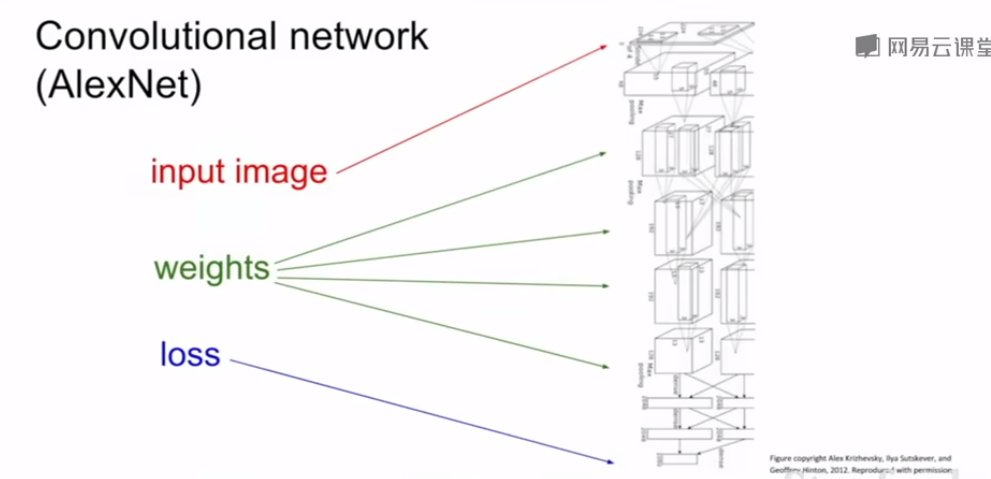
# 图示解读

  1. 输入图像（input image):
    • 输入的一般是原始 RGB 彩色图像，输入到卷积神经网络进行处理
  2. 权重：
    • 绿色箭头表示网络的权重
    • 权重是模型的可训练参数，在每一层中应用不同的卷积核来提取特征
    • AlexNet 中的权重在每一层都起着关键作用，通过训练不断调整以优化模型性能
  3. 损失：
    • 蓝色箭头表示损失函数
    • 损失函数用于衡量模型预测与实际标签之间的差异，并指导模型权重的更新。

# AlexNet 结构

AlexNet 是一种深度卷积神经网络，因在 2012 年的 ImageNet 竞赛中取得了显著成果而闻名。图中展示了 AlexNet 的典型结构，包括以下几个主要部分：

卷积层（Convolutional Layers）：

  • 每个卷积层使用多个卷积核对输入进行卷积操作，提取局部特征。
  • 卷积操作包括卷积核与输入的局部区域进行点积运算，生成特征图（Feature Map）。

激活函数（Activation Functions）：

  • 通常使用 ReLU（Rectified Linear Unit）激活函数，对卷积层输出进行非线性变换，增强模型的表达能力。

池化层（Pooling Layers）：

  • 池化层通过下采样操作（如最大池化）减少特征图的尺寸，保留重要特征，同时减少计算量和参数量。

全连接层（Fully Connected Layers）：

  • 在卷积层和池化层之后，连接一系列全连接层，将高维特征映射到分类空间。
  • 全连接层的输出通过 Softmax 函数转换为各类别的概率分布。

输出层（Output Layer）：

  • 输出层产生最终的预测结果，通常是图像分类任务中的类别概率。

# 训练过程

前向传播（Forward Propagation）：

  • 输入图像经过网络层层处理，产生预测结果。
  • 计算损失函数，衡量预测结果与真实标签之间的误差。

反向传播（Backward Propagation）：

  • 通过计算损失函数对每个参数的梯度，指导权重更新。
  • 使用优化算法（如梯度下降）更新权重，使损失函数逐渐减小。

迭代训练：

  • 重复前向传播和反向传播，迭代训练模型，直到损失函数收敛或达到预设的训练轮数。

# 训练图

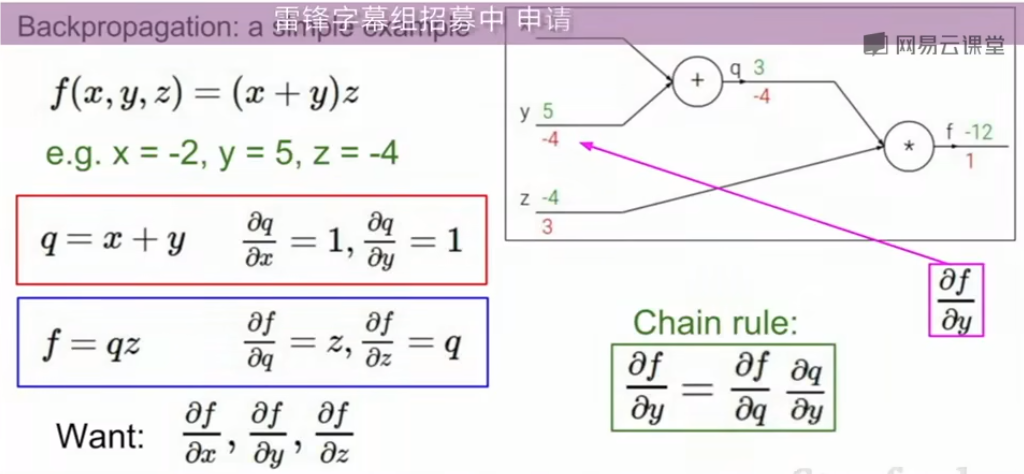
QQ_1721026645644.png

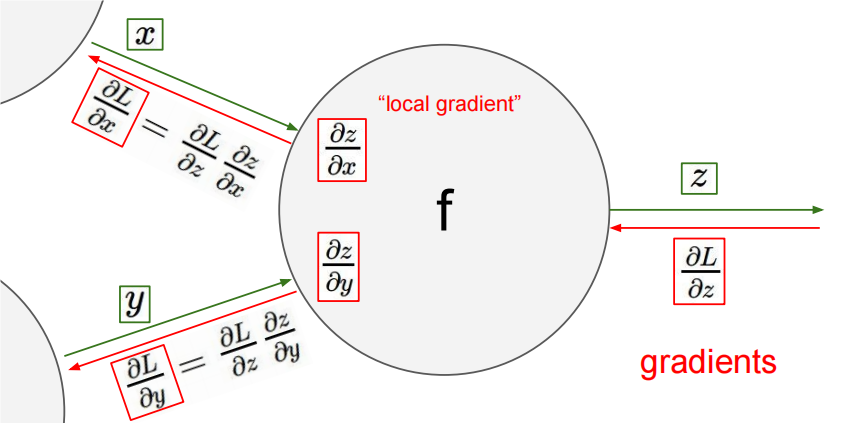
QQ_1721029349549.png

# 反向传播中的梯度计算

反向传播是深度学习中计算梯度的一种高效方法，通过链式法则（Chain Rule）逐层传递梯度，从而计算出损失函数相对于每个参数的导数。

# 函数ff 的输入和输出：

  • ff 是一个复合函数，输入为x和yx和y，输出为zz
  • 最终希望计算损失函数LL 相对于输入xx 和yy 的梯度

# 局部梯度：

  • 局部梯度是指函数ff 对其输入变量的偏导数:

    ∂z∂x,∂z∂y\begin{aligned}\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}\end{aligned}

  • 这些局部梯度反映了xx 和yy 如何影响中间变量zz

# 全局梯度

  • 全局梯度是指损失函数LL 对输入变量xx 和yy 的偏导数:

    ∂L∂x,∂L∂y\frac{\partial L}{\partial x},\frac{\partial L}{\partial y}

  • 这些梯度通过链式法则计算，结合局部梯度和损失函数对输出zz 的梯度：

    ∂L∂z\frac{\partial L}{\partial z}

# 链式法则的运用

# 对xx 的梯度计算

  • 通过链式法则，损失函数LL 对xx 的梯度为:

    ∂L∂x=∂L∂z⋅∂z∂x\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\cdot\frac{\partial z}{\partial x}

  • ∂L∂x\frac{\partial L}{\partial x} 是从后面的层传递过来的梯度，表示损失函数LL 对zz 的梯度

  • ∂z∂x\frac{\partial z}{\partial x} 是局部梯度，表示zz 对xx 的偏导数

# 对yy 的梯度计算

  • 损失函数LL 对yy 的梯度为：

    ∂L∂y=∂L∂z⋅∂z∂y\begin{aligned}\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z}\cdot\frac{\partial z}{\partial y}\end{aligned}

# 反向传播流程图

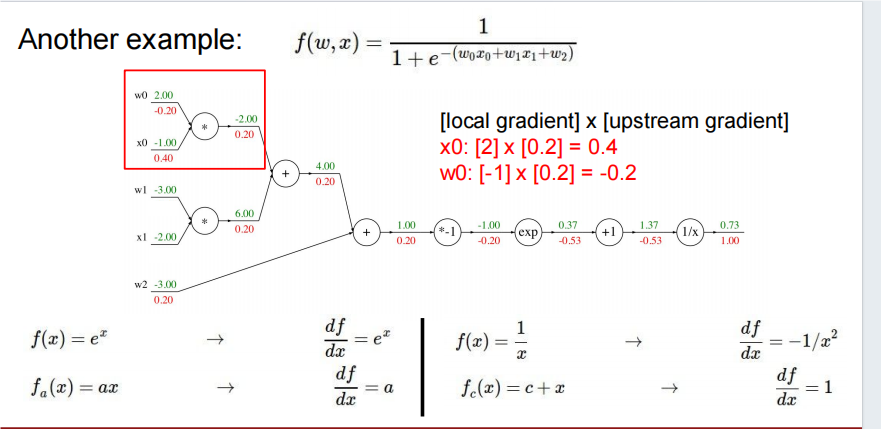
image.png

函数f(w,x)f(w,x) 定义为:

f(w,x)=11+e−(w0x0+w1x1+w2)f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}}

这是一个典型的逻辑回归模型，其输出是一个概率值，表示输入 $ x $ 属于某一类别的概率。

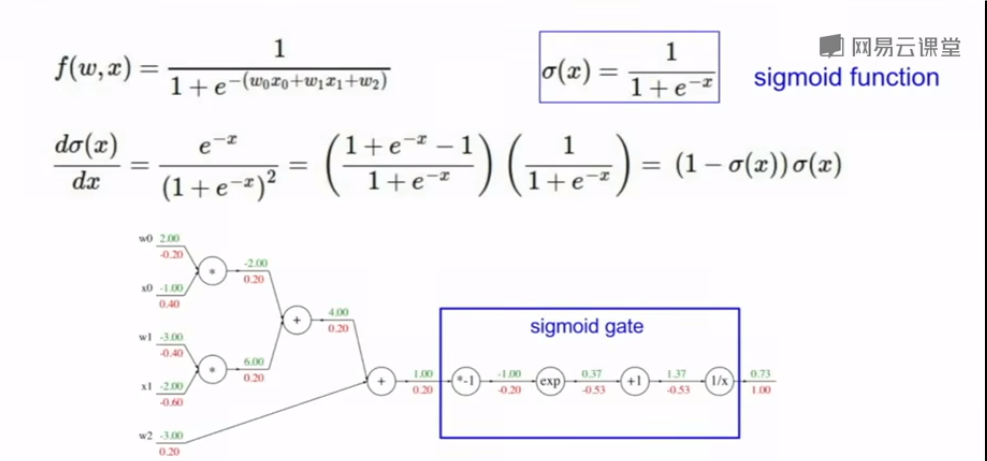
QQ_1721034743182.png

基础公式:

σ(x)=11+e−xdσ(x)dx=e−x(1+e−x)2=(1+e−x−11+e−x)(11+e−x)=(1−σ(x))σ(x)\sigma(x)=\frac1{1+e^{-x}}\\ \frac{d\sigma(x)}{dx}=\frac{e^{-x}}{\left(1+e^{-x}\right)^2}=\left(\frac{1+e^{-x}-1}{1+e^{-x}}\right)\left(\frac1{1+e^{-x}}\right)=\left(1-\sigma(x)\right)\sigma(x)