import numpy as np

class NearestNeighbor:
    def __init__(self):
        pass

    def train(self, X, y):
        """ X is N x D where each row is an example. Y is 1-dimension of size N """
        # the nearest neighbor classifier simply remembers all the training data
        self.Xtr = X
        self.ytr = y

    def predict(self, X):
        """ X is N x D where each row is an example we wish to predict label for """
        num_test = X.shape[0]
        # lets make sure that the output type matches the input type
        Ypred = np.zeros(num_test, dtype=self.ytr.dtype)

        # loop over all test rows
        for i in range(num_test):
            # find the nearest training image to the i'th test image
            # using the L1 distance (sum of absolute value differences)
            distances = np.sum(np.abs(self.Xtr - X[i,:]), axis=1)
            min_index = np.argmin(distances)  # get the index with smallest distance
            Ypred[i] = self.ytr[min_index]    # predict the label of the nearest example

        return Ypred

# 示例使用
if __name__ == '__main__':
    # 创建一些示例数据
    Xtr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])  # 训练数据
    ytr = np.array([0, 1, 2])  # 训练标签

    Xte = np.array([[1, 2, 3], [4, 5, 5], [7, 7, 9]])  # 测试数据

    # 初始化和训练分类器
    nn = NearestNeighbor()
    nn.train(Xtr, ytr)

    # 预测测试数据的标签
    Yte_predict = nn.predict(Xte)
    print('Predicted labels:', Yte_predict)

# 本项目参考学习文档为斯坦福计算机深度学习课程 —— 用于视觉识别的 CS231n 卷积神经网络

曼哈顿距离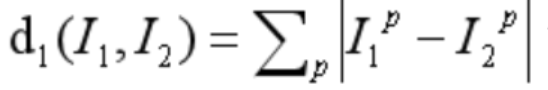：，其中 I1 和 I2 是两幅图像，I1P 和 I2P 分别是 I1 和 I2 在位置 P 的像素值。差异矩阵也是像素点依次相减。通过衡量图像像素点的绝对值差之和差异性来

对于该预测方法还有 L2 距离，其定义为：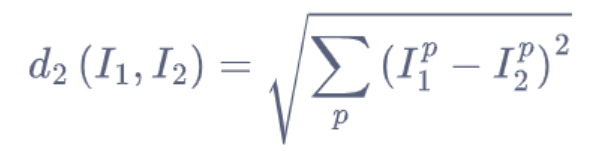

最近临分类器：
（1）训练：将训练数据存储在实际变量中。
（2）预测：对每一个测试样本，计算其与训练样本 L1 的距离，找到距离最近的训练样本，将该训练样本的标签作为测试样本的预测标签。
* 训练方法 ：def train (self, X, y): X（训练数据，形状为 ND，每一行都是一个样本）和 y（训练标签，大小为 N 的一维数组）, 然后存储在 self 类中。

self.Xtr = X

self.ytr = y

预测方法

predict 方法接受一个参数 x*(测试数据，形状为 N*D，每一行都是一个需要预测的样本)*

num_test 表示测试样本的数量

Ypred 初始化为零数组 np.zeros(num_test,dtype=self.ytr.dtype) , 前者表示数组的长度，即为包含元素的个数；后者是一个关键词参数，指定数组中的数据类型设置为与 self.ytr 数组的数据类型相同。dtype 是数据类型的缩写。

对于每个测试样本，计算它与所有训练样本的 L1 距离：

1	distances = np.sum(np.abs(self.Xtr - X[i,:]), axis=1)

通过取绝对值差的和计算 L1 距离。
self.Xtr - X[i,:] 计算每个训练样本与第 i 个测试样本的差值。(这里 self.Xtr 是一个矩阵， X[i,:] 是一个向量 X[i,:] 表示矩阵 X 的第 i 行)
self.Xtr - X[i,:] 计算的是矩阵 self.Xtr 中的每一行向量减去向量 X[i,:] 的结果。
np.abs(self.Xtr - X[i,:]) ：对上述差值矩阵中的每个元素取绝对值，得到一个与 self.Xtr 形状相同的矩阵。
np.sum(..., axis=1) 对每个样本的所有特征求和，得到每个训练样本与该测试样本的距离。
通过 min_index = np.argmin(distances) 找到距离最小的样本 (np.argmin: 返回最小距离对应的索引)

Q: With N examples, how fast are training and prediction?

问题：对于 N 个样本，训练和预测的速度（效率）是多少？

A: Train O(1), predictO(N)

回答：训练时间复杂度是 O (1)，预测时间复杂度是 O (N)。
训练时间复杂度 O (1)：训练阶段只需记住所有训练数据，不需要复杂计算，所以训练时间是常数时间，即与训练样本的数量 N 无关。
预测时间复杂度 O (N)：预测阶段，对于每个测试样本，需要计算其与所有训练样本的距离，并找到最近的那个训练样本。因此，预测时间与训练样本的数量 N 成正比。

Q:This is bad: we want classifiers that are fast at prediction; slow for training is ok

为什么这是不好的设计？

A: 这是不好的设计：我们希望分类器在预测时速度快；在训练时速度慢是可以接受的。

在实际应用中，预测阶段通常比训练阶段更频繁。例如，一个已经训练好的分类器可能需要处理大量的实时预测请求。如果预测速度很慢，会严重影响系统的性能和用户体验。
训练阶段可以相对较慢，因为训练通常是一个离线过程，可以在后台完成，不直接影响用户体验。

# 总结

最近邻分类器的一个主要缺点是它的预测阶段计算量大，对于每个测试样本需要计算其与所有训练样本的距离，因此预测速度较慢。这在需要快速响应的应用中是一个很大的问题，而对于训练阶段的速度要求则相对宽松。因此，更理想的分类器设计是训练阶段可以慢一些，但预测阶段必须非常快。

# K - 最近临法

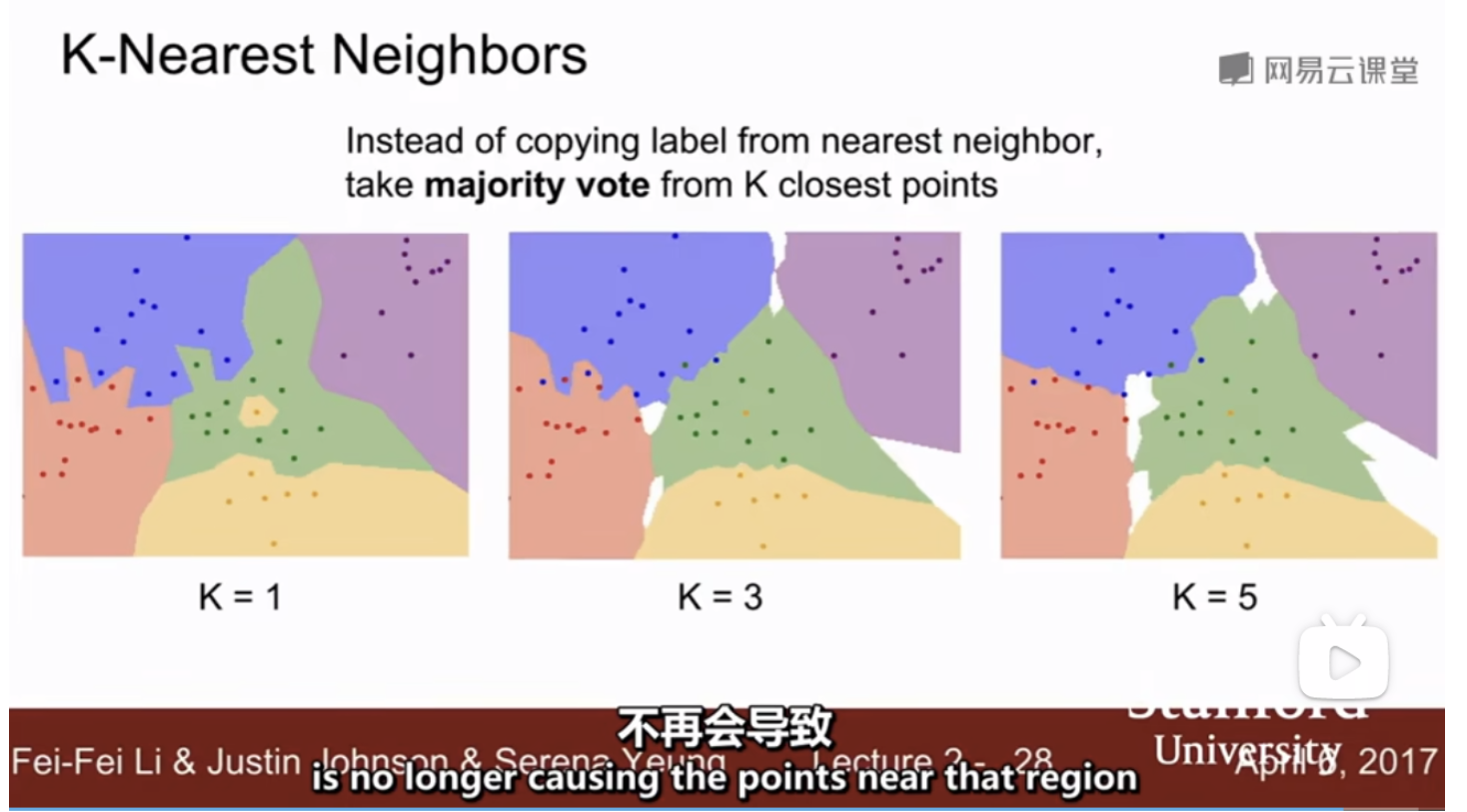
图中展示的是 K - 最近邻（K-Nearest Neighbors, K-NN）分类器的基本原理和效果。K-NN 分类器是一个简单但非常有效的分类算法，它的核心思想是根据一个样本的 K 个最近邻居来确定其类别。具体来说，这里通过 K 个最近邻居的多数投票来决定样本的分类。

白色区域：这个区域没有进行 k - 最近投票

k=1：

当 K=1 时，分类器仅考虑与样本最近的一个邻居。这个邻居的类别直接决定了样本的类别。虽然这种方法非常直接和简单，但它容易受噪声和孤立点的影响，导致分类效果不稳定。

k=3：

当 K=3 时，分类器考虑与样本最近的三个邻居。样本的类别由这三个邻居的多数投票决定。相比于 K=1，这种方法更加鲁棒，能够更好地抵御噪声的影响。但是，它仍然可能受少数几个错误邻居的影响。

k=5：

当 K=5 时，分类器考虑与样本最近的五个邻居。样本的类别由这五个邻居的多数投票决定。进一步增加 K 值，分类器变得更加稳定，因为它综合了更多邻居的信息，减少了单个噪声点对分类结果的影响。然而，如果 K 值过大，分类器可能会包含过多不相关的邻居信息，导致分类结果不准确。

# 主要思想

多数投票：K-NN 分类器的核心思想是 “多数投票”，即根据 K 个最近邻居中出现频率最高的类别来决定样本的类别。
距离度量：K-NN 分类器依赖于距离度量来确定最近的 K 个邻居。常用的距离度量方法包括欧氏距离、曼哈顿距离等。
参数选择：K 值的选择对分类效果有重要影响。K 值太小容易受噪声影响，K 值太大则可能引入过多无关信息。

# 接下来我们以 CIFAR-10 数据集的结果来进行代码编写

import numpy as np
import pickle  #用于序列化和反序列化 Python 对象的库。在这里用于加载 CIFAR-10 数据集文件
import os
from sklearn.model_selection import KFold

def load_CIFAR_batch(filename):
    """ Load a single batch of CIFAR-10 """
    with open(filename, 'rb') as f: #以二进制模式('rb')打开文件
        datadict = pickle.load(f, encoding='latin1')  #使用pickle.load(f,encoding='latin1')反序列化文件内容，读取为字典对象
        X = datadict['data']
        Y = datadict['labels']
    #将其从平坦形状(10000,3072)重塑为(10000,32,32,3),并且将数据类型转为浮点型。即10000张图
    # 每张图有32*32像素，每个像素有三个颜色通道
    #并且将像素类型转为浮点数
        X = X.reshape(10000, 32, 32, 3).astype('float')
        Y = np.array(Y)
        return X, Y

def load_CIFAR10(ROOT): #ROOT表示CIFAR-10数据集根目录的路径
    """ Load all of CIFAR-10 """
    xs = [] #存储每个批次的图像数据
    ys = [] #存储每个批次的标签
    for b in range(1, 6): #加载五个训练批次
        f = os.path.join(ROOT, 'data_batch_%d' % (b,))  #依次加载文件里的五个批次
        X, Y = load_CIFAR_batch(f)  #调用load_CIFAR_batch（）函数来加载数据
        #将加载的的图像数据和标签分别添加到列表中
        xs.append(X)
        ys.append(Y)
    #将所有训练批次的数据合并为一个训练集
    Xtr = np.concatenate(xs)
    Ytr = np.concatenate(ys)
    del X, Y    #释放内存，删除X和Y
    Xte, Yte = load_CIFAR_batch(os.path.join(ROOT, 'test_batch')) #加载测试批次的数据
    return Xtr, Ytr, Xte, Yte

# 加载数据
Xtr, Ytr, Xte, Yte = load_CIFAR10(r'D:\desktop\Code_Compiling\cs231n_stanford\example&tests\cifar-10-python\cifar-10-batches-py')
# 将数据拉成向量
#重塑数据：将训练数据 Xtr 和测试数据 Xte 从形状（num_samples, 32, 32, 3）转换为（num_samples, 3072）的向量形式
# 其中 3072 是 32x32 图像的像素总数乘以 3 个颜色通道。
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3)
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3)

print("数据加载和预处理完成")

class NearestNeighbor:
    def __init__(self): #初始化
        pass

    def train(self, X, y):  #该方法用于训练k-NN模型，将x和y存储为类的属性
        """ X is N x D where each row is an example. Y is 1-dimension of size N """
        self.Xtr = X    #X是N*D的矩阵，每行是一个训练样本
        self.ytr = y    #y是一个长度为N的一维数组，对应于每个训练样本的标签

    #预测给定的数据集x的标签,X是N*D的矩阵，每行都是一个测试样本
    #k是要考虑的最近邻居的数量，默认为1。distfn是距离度量方式，可以是：L1(曼哈顿距离)也可以是L2(欧几里得距离)
    def predict(self, X, k=1, distfn='L1'):
        """ X is N x D where each row is an example we wish to predict label for """
        num_test = X.shape[0]   #这是测试集的样本数量
        Ypred = np.zeros(num_test, dtype=self.ytr.dtype)    #初始化为一个零数组，用于存储每个测试样本的预测标签
        #循环处理每个测试样本
        for i in range(num_test):
            if distfn == 'L1':
                distances = np.sum(np.abs(self.Xtr - X[i,:]), axis=1)
            elif distfn == 'L2':
                distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis=1))
            min_indices = np.argpartition(distances, k)[:k] #找到k个最近邻居的索引
            closest_y = self.ytr[min_indices]
            #预测标签
            #使用 np.bincount 统计最近邻居中每个标签的出现次数，并选择出现次数最多的标签作为预测标签。
            Ypred[i] = np.bincount(closest_y).argmax()

        return Ypred

# 训练和评估模型
nn = NearestNeighbor()  #创建 NearestNeighbor 类的实例 nn。
nn.train(Xtr_rows, Ytr) #使用训练数据 Xtr_rows 和标签 Ytr 训练模型。
Yte_predict = nn.predict(Xte_rows)  #使用测试数据 Xte_rows 预测标签。
print('accuracy: %f' % (np.mean(Yte_predict == Yte)))   #计算并打印预测标签与真实标签的匹配率（准确率）。

# 创建验证集——从训练集中提取前1000个样本作为验证集
Xval_rows = Xtr_rows[:1000, :]  #验证集特征
Yval = Ytr[:1000]   #验证集标签
Xtr_rows = Xtr_rows[1000:, :]   #新训练集特征
Ytr = Ytr[1000:]    #新训练集标签

# 超参数调优——对于不同的k和距离度量方式进行超参数调优
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
    for distfn in ['L1', 'L2']:
        nn = NearestNeighbor()  #创建NearestNeighbor实例
        nn.train(Xtr_rows, Ytr) #训练
        Yval_predict = nn.predict(Xval_rows, k=k, distfn=distfn)    #预测
        acc = np.mean(Yval_predict == Yval) #验证
        print(f'accuracy for k={k}, distfn={distfn}: {acc}')
        validation_accuracies.append((k, distfn, acc))
#交叉验证函数
def cross_validation(X, y, k_choices, distfns):
    kf = KFold(n_splits=5)  #将数据集分成五份
    validation_accuracies = []
    for k in k_choices: #对每个k和distfns组合进行操作
        for distfn in distfns:
            accs = []   #初始化一个空列表 accs 用于存储交叉验证的准确率
            for train_index, val_index in kf.split(X):
                X_train, X_val = X[train_index], X[val_index] #将数据分为训练集和验证集。
                y_train, y_val = y[train_index], y[val_index]

                nn = NearestNeighbor()
                nn.train(X_train, y_train)
                y_val_predict = nn.predict(X_val, k=k, distfn=distfn)
                acc = np.mean(y_val_predict == y_val) #用验证集进行预测并计算准确率。
                accs.append(acc)
            avg_acc = np.mean(accs)#计算并打印每个 k 和 distfn 组合的平均准确率。
            validation_accuracies.append((k, distfn, avg_acc))#将 k、distfn 和平均准确率保存到 validation_accuracies 列表中。
            print(f'Cross-validation accuracy for k={k}, distfn={distfn}: {avg_acc}')
    return validation_accuracies

# 使用交叉验证
k_choices = [1, 3, 5, 10, 20, 50, 100]
distfns = ['L1', 'L2']
validation_accuracies = cross_validation(Xtr_rows, Ytr, k_choices, distfns)

k-NN 阶段实现了一个简单的 k 近邻（k-Nearest Neighbors, k-NN）分类器，使用了 L1 距离（曼哈顿距离）和 L2 距离（欧几里得距离）

代码注释已列与代码中

# 本项目参考学习文档为斯坦福计算机深度学习课程 —— 用于视觉识别的 CS231n 卷积神经网络

# 总结

# K - 最近临法

# 主要思想

# 接下来我们以 CIFAR-10 数据集的结果来进行代码编写

k-NN最近分类器_Sanfordcs231n

组合逻辑基础模块