Home HKUST_RA

# GNN

  • V: Vertex (or node) attributes
  • E: Edge (or link) attributes and directions
  • U: Global (or master node) attributes

# How to express a graph?

  • 图的邻接矩阵
  • Adjacency List：（2*N）的矩阵，2 表示 source 和 target
  • 如何更新点的特征？
    • 考虑自身信息
    • 考虑邻居节点信息

# 聚合方法

m=G(Wj∗xi:j∈Ni)m=G({W_j * x_i:j \in \mathcal N_i})

hi=σ(W1∗hi+∑j∈NW2∗hi)h_i=\sigma (W_1 * h_i + \sum_{j \in \mathcal N}W_2*h_i)

(1) 式用于结合邻居与自身信息，其中的 $ W_j * x_i $ 表示结合邻居信息，(2) 式表示汇总

  • GNN 本质：更新各部分特征
  • 其中输入是特征，输出也是特征
  • 多层 GNN—— 可以更好的吸收全局变量，得到更多节点的特征

# Stanford CS224W

# 聚类系数

聚类系数衡量了节点 $ v 的邻居节点之间相互连接的概率。它用的邻居节点之间相互连接的概率。它用 e_v$ 表示，代表了邻居节点之间实际存在的边数与可能存在的边数的比例。

ev=#(邻居节点间的边数)(kv2)∙其中,kv表示节点v的邻居节点数量,(kv2)代表邻居节点之间可能形成的边对数量。e_v=\frac{\#(\text{邻居节点间的边数})}{\binom{k_v}2}\\\bullet\quad\text{其中,}k_v\text{ 表示节点 }v\text{ 的邻居节点数量,}\binom{k_v}2\text{ 代表邻居节点之间可能形成的边对数量。}

# Katz 指数 (Katz index)

Katz(u,v)=∑k=1∞βk⋅(Ak)uvKatz(u,v)=\sum_{k=1}^\infty\beta^k\cdot(A^k)_{uv}

  • 它会考虑两个节点之间的直接路径（即较短的路径）和较长的路径，而不仅仅是最短路径。
  • 有助于衡量节点之间的整体连通性，尤其是在复杂网络中，通过考虑长度不同的路径来判断节点之间的潜在关系

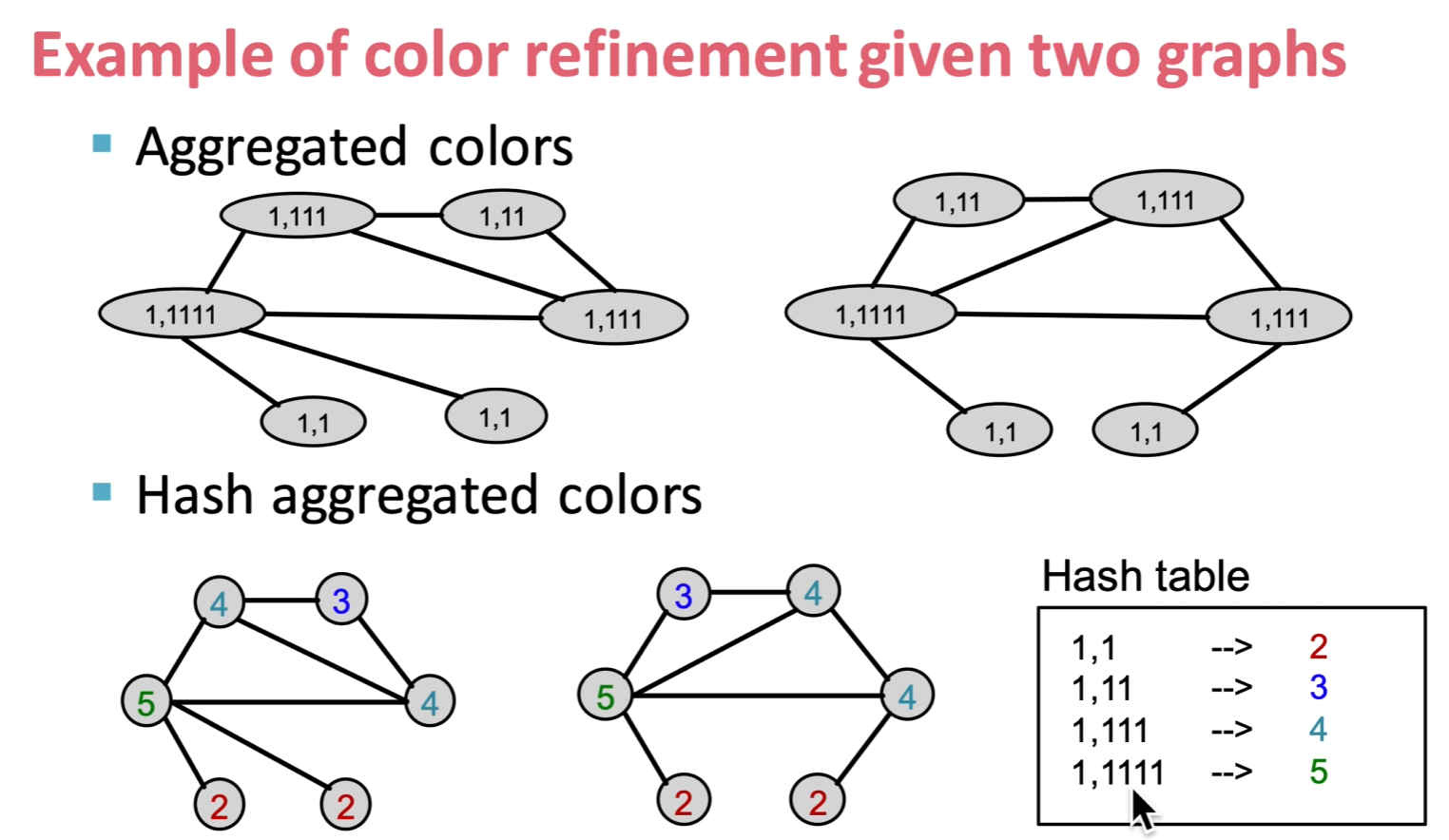
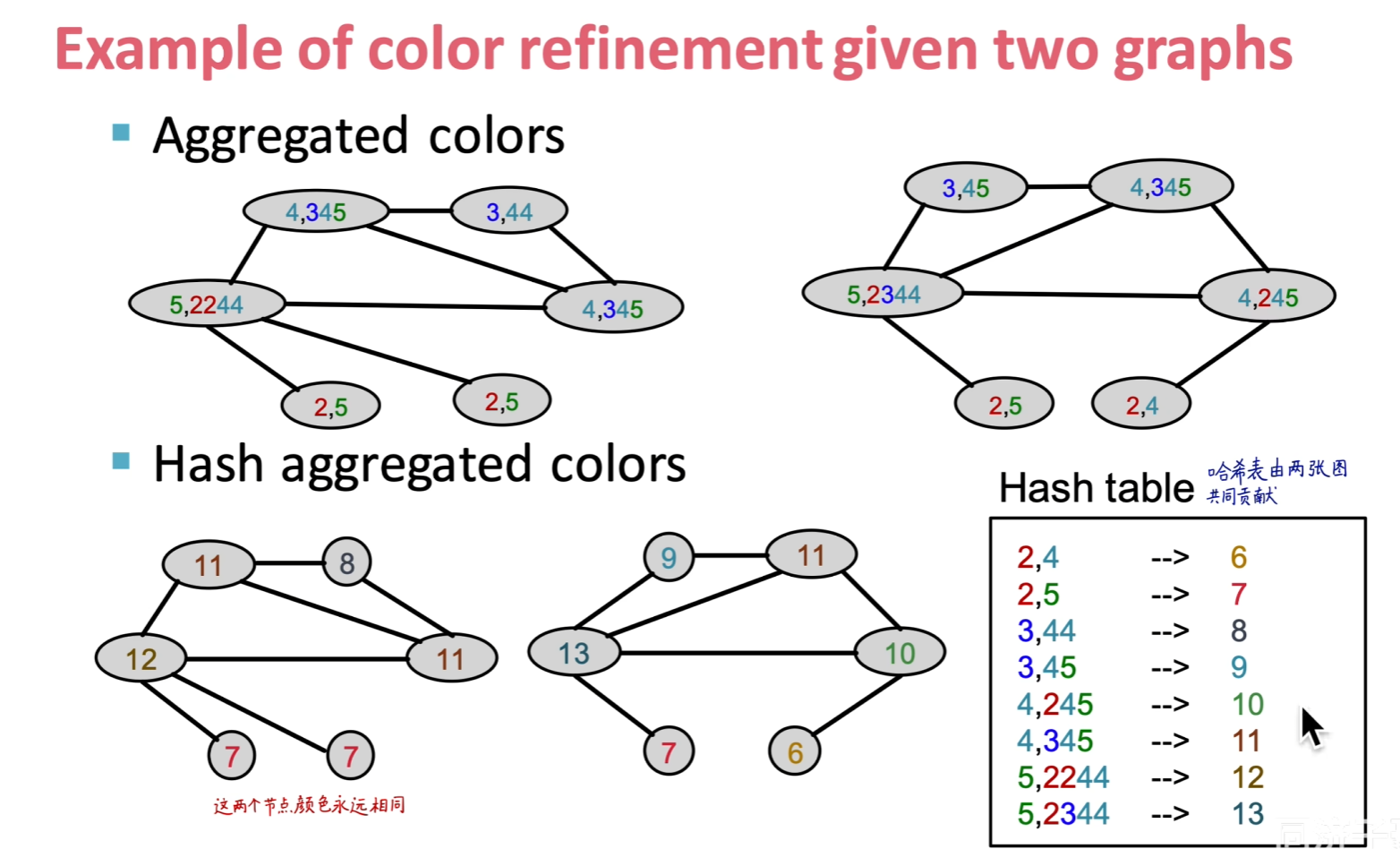
# Hash

image.png

image.png

# 图相似性

similarity in embedding space(u,v)=zuTzv\text{similarity in embedding space}(u,v)=z_u^Tz_v

内积计算： 内积是一种衡量两个向量相似性的度量，它可以通过以下公式计算：

zuTzv=∑i=1dzu(i)zv(i)z_u^Tz_v=\sum_{i=1}^dz_u^{(i)}z_v^{(i)}

# 编码器

# 基于随机游走的编码器

# DeepWalk

原理：DeepWalk 方法使用 随机游走（Random Walk） 来捕捉图中局部的节点邻居关系。随机游走是一种模拟从某一节点出发，按概率遍历其邻居节点的过程。

过程：

  1. 对每个节点执行多次随机游走，生成多个 “邻居序列”。
  2. 将这些序列看作一个类比于自然语言中的句子，并使用 word2vec 技术（如 Skip-gram 模型）对序列进行训练，最终输出节点的嵌入向量。
  3. 通过优化 word2vec 的目标函数（即最大化节点与其随机游走邻居节点的同现概率），学习到每个节点的嵌入表示。

编码器过程：

  • DeepWalk 通过使用 word2vec 类似的方法，将图中的节点 “编码” 到一个低维的向量空间中，使得距离相近的节点在嵌入空间中也较为接近。

# Node2Vec

原理：Node2Vec 是 DeepWalk 的扩展。它在随机游走的过程中引入了更灵活的跳转机制，可以控制随机游走时是更多地向局部探索（DFS），还是全局探索（BFS）。

过程：

  1. 在执行随机游走时，引入两个参数 p 和 q ，控制游走偏向局部还是全局。
  2. 使用和 DeepWalk 类似的 word2vec 方法对生成的序列进行训练，学习节点的嵌入向量。

# 基于矩阵分解的编码器

# Laplacian Eigenmaps

原理：Laplacian Eigenmaps 是一种经典的基于图拉普拉斯矩阵（Laplacian matrix）的图嵌入方法。它通过最小化节点在低维空间中距离的平方差，保持节点的局部结构。

过程：

  1. 构建图的拉普拉斯矩阵L=D−AL = D - A（其中 $ A是邻接矩阵，是邻接矩阵，D$ 是度矩阵）。
  2. 通过对拉普拉斯矩阵进行特征值分解，获得最小的 $ k$ 个特征值和对应的特征向量。
  3. 这些特征向量就是节点在低维嵌入空间中的表示，特征向量的维度就是嵌入维度。

# 随机游走

m=⌈2ϵ2(log⁡(2η−2)−log⁡(δ))⌉m=\left\lceil\frac{2}{\epsilon^2}\left(\log(2\eta-2)-\log(\delta)\right)\right\rceil

  • ηη 是长度为 $ l$ 的匿名游走总数。
  • ϵ\epsilon 是我们希望误差小于的值。
  • δ\delta 是我们允许的最大概率错误。

# 方法介绍

  • 从每个节点uu 出发，运行TT 次不同的随机游走，每个游走的长度为ll
  • 这些随机游走的集合记作：NR(u)={w1u,w2u,…,wTu}N_{R}(u)=\{w_{1}^{u},w_{2}^{u},\ldots,w_{T}^{u}\}
  • 目标是预测哪些游走在某个窗口内一起出现，这种共现信息可以帮助捕捉随机游走之间的相似性和图结构中高阶的联系。

# 目的

  • 最大化以下函数：

    max⁡Z,d1T∑t=1T−Δlog⁡P(wt∣wt−Δ,…,wt+Δ,zG)\max_{Z,d}\frac{1}{T}\sum_{t=1}^{T-\Delta}\log P(w_{t}\mid w_{t-\Delta},\ldots,w_{t+\Delta},z_{G})

  • 通过最大化游走嵌入的对数概率，来学习使得在窗口ΔΔ 内共现的游走嵌入向量能够相互预测。

  • 共现概率为：

    P(wt∣wt−Δ,…,wt+Δ,zG)=exp⁡(y(wt))∑i=1ηexp⁡(y(wi))P(w_t\mid w_{t-\Delta},\ldots,w_{t+\Delta},z_G)=\frac{\exp(y(w_t))}{\sum_{i=1}^\eta\exp(y(w_i))}

    其中，y(wt)y(w_t) 是wtw_t 的评分函数

  • 评分函数算法：

    y(wt)=b+U⋅(cot⁡(12Δ∑i=t−Δt+Δzi,zG))y(w_t)=b+U\cdot\left(\cot\left(\frac{1}{2\Delta}\sum_{i=t-\Delta}^{t+\Delta}z_i,z_G\right)\right)

    • 其中，ztz_t 是游走的嵌入向量，zGz_G 是图的全局嵌入
    • 评分函数结合了游走嵌入向量ziz_i 和图的全局嵌入zGz_G，表示游走之间和图全局的关系

# GCN

# 计算

  • 邻接矩阵AA 归一化

    A^=D~−1/2A~D~−1/2\hat A=\tilde D^{-1/2}\tilde A\tilde D^{-1/2}

    • 这里的A^\hat A 是计算公式为A^=A+I\hat A=A+I
    • 度矩阵D^\hat D: 是一个对角矩阵，表示图中每个节点的度数（即每个节点有多少个直接相连的邻居）

  • GCN 层计算:

    Z=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))Z=f(X,A)=\mathrm{softmax}(\hat{A} \mathrm{ReLU}(\hat{A}XW^{(0)})W^{(1)})

  • XX 是输入特征矩阵，每一行代表一个节点的特征，大小为 N×CN \times C（节点数量 $ N 和特征维度和特征维度 C$）。

    W(0)W^{(0)} 是可训练的权重矩阵，用于第一次线性变换，大小为 C×HC \times H，将输入特征从 $C 维映射到隐藏层维映射到隐藏层 H $ 维。

    A^\hat{A} 是归一化后的邻接矩阵，用来对特征进行消息传递（message passing），使得节点从邻居处接收信息。

    ReLU\text{ReLU} 是激活函数，确保非线性。

    W(1)W^{(1)} 是第二层的权重矩阵，将隐藏层映射到输出层的特征维度，大小为 $ H \times F$。

    最终经过 Softmax 函数输出分类结果。