Home deep-learning

image.png

# INTRODUCTION

# 介绍

  • 图数据的复杂性对现有的机器学习算法提出了重大挑战：
    • 图可以是不规则的
    • 一个图可能有不同大小的无序节点
    • 来自一个图的节点可能有不同数量的邻居
    • 一些重要的操作 (如卷积) 在图像域很容易计算，但很难应用到图域

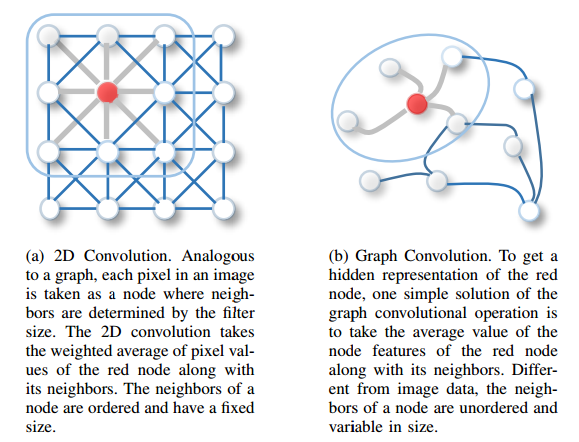
image.png

  • 二维卷积：在二维卷积中，图像被视为一个规则的网格，每个像素点是一个节点，像素点之间的连接形成了一个规则的邻域结构。二维卷积操作的基本步骤包括：

    • 在二维卷积中，通过一个滤波器（filter）在图像上滑动，取红色节点及其邻居节点的像素值的加权平均值。这些邻居节点是有序且大小固定的。
    • 滤波器的大小通常是固定的（例如 3x3），它在图像上滑动的过程中，产生了对图像的局部特征提取。

  • 图卷积将二维卷积的思想推广到一般的图结构上，图结构可以是任何形式的节点和边的连接。图卷积的基本原理包括以下几个步骤：

    1. 邻居信息聚合：
      • 对于图中的每一个节点，图卷积会从该节点的邻居节点中聚合信息。邻居节点可以是直接与该节点相连的其他节点。
      • 聚合方式可以是加权平均、求和或最大值等操作。比如，如果使用加权平均，图卷积会考虑每个邻居节点的特征，并根据边的权重进行加权。
    2. 特征更新：
      • 聚合完邻居节点的信息后，该节点的特征将被更新为聚合信息的结果。这个更新过程类似于二维卷积中的特征提取，即将邻域信息整合进来，生成新的节点表示。
      • 更新过程可以通过一个线性变换（例如矩阵乘法）和一个非线性激活函数（如 ReLU）来实现，使得模型能够学习到复杂的特征表示。
    3. 堆叠多个卷积层：
      • 为了捕捉更高层次的特征表示，可以堆叠多个图卷积层。每一层都会进一步聚合更广泛的邻居信息，从而捕捉到更多的图结构信息。
      • 多层的图卷积可以看作是在更深的网络中传递和更新节点特征，使得最终的节点表示能够包含全局图结构的信息。

  • 基本数学公式表达：

    H(l+1)=σ(D−1AH(l)W(l))H^{(l+1)}=\sigma(D^{-1}AH^{(l)}W^{(l)})

    其中：

    • AA 是图的邻接矩阵，表示图中节点之间的连接关系。
    • $D $ 是度矩阵，表示每个节点的度数（即有多少个邻居）。
    • H(l)H^{(l)} 是第 $ l $ 层的节点特征矩阵。
      • 特征矩阵（Feature Matrix）是图神经网络（GNN）中的一个关键概念，它用于表示图中每个节点的属性或特征。在不同的任务中，特征矩阵的具体形式和含义可能会有所不同，但其核心思想是为图中的每个节点分配一组数值，来描述该节点的属性或状态。
      • 通常由符号 X 表示，大小为n×dn × d,nn 是图中节点的数量，dd 是每个节点的特征维度，即每个节点由dd 个数值来描述
      • 在社交网络中，节点可能代表用户，每个用户的特征可以包括用户的年龄、性别、兴趣、所在城市等。如果有 5 个用户（节点），每个用户的特征用 3 个属性表示（例如年龄、性别和城市），那么特征矩阵的维度为5×35 \times 3。
    • W(l)W^{(l)} 是第 $ l$ 层的权重矩阵。
    • σ\sigma 是激活函数（如 ReLU），用于引入非线性。

# 定义

# 1. 图（Graph）的定义

  • 图（Graph）： 图可以表示为G=(V,E)G = (V, E)，其中 $ V是节点的集合，是节点的集合，E $ 是边的集合。图中的节点用 viv_i 表示，边用eij=(vi,vj)e_{ij} = (v_i, v_j) 表示，这表示从节点vjv_j 指向viv_i 的一条边。
  • 邻居（Neighborhood）： 节点 $ v 的邻居定义为的邻居定义为 N (v) = { u \in V | (v, u) \in E }，表示与节点，表示与节点 v$ 相连的所有节点的集合。
  • 邻接矩阵（Adjacency Matrix）： 邻接矩阵 $ A $ 是一个 n×nn \times n 的矩阵，其中 Aij=1A_{ij} = 1 表示存在从 vjv_j 到 viv_i 的边，否则 Aij=0A_{ij} = 0。
  • 节点特征矩阵（Node Feature Matrix）： 图中的节点可能会有属性（特征），用 XX 表示。 是一个 n×dn \times d 的矩阵，其中 xvx_v 是节点 vv 的特征向量，维度为 dd。
  • 边特征矩阵（Edge Feature Matrix）： 边也可能有属性，用 XeX^e 表示。XeX^e 是一个 m×cm \times c 的矩阵，其中 xv,uex_{v,u}^e 是边 (v,u)(v, u) 的特征向量，维度为 cc。

# 2. 方向图（Directed Graph）的定义

  • 方向图： 一个方向图是指其所有的边都有方向的图结构。无向图可以看作是方向图的一个特例，其中每对相连节点之间有一对方向相反的边。
  • 邻接矩阵的对称性： 如果邻接矩阵是对称的，则图为无向图。

# 3. 时空图（Spatial-Temporal Graph）的定义

  • 时空图： 时空图是一种带有属性的图，其中节点的属性（特征）会随着时间动态变化。时空图表示为 G(t)=(V,E,X(t))G^{(t)} = (V, E, X^{(t)})，其中X(t)X^{(t)} 是节点在时间tt 的特征矩阵。

# 图神经网络分类

# 1. 递归图神经网络（Recurrent Graph Neural Networks, RecGNNs）

# 1.1 基本原理

  • RecGNNs 的核心思想是通过递归地传播信息来学习节点的表示。每个节点会不断地从它的邻居那里接收信息并更新自身的状态，直到整个图达到某种稳定的平衡状态（即所有节点的表示不再发生显著变化）。
  • 这种信息传播的过程类似于经典的递归神经网络（RNN），但它在图结构上进行操作。

# 1.2 公式

RecGNNs的节点更新公式通常表示为:hv(t)=f(xv,∑u∈N(v)g(hu(t−1),x(v,u)))其中:∙hv(t)是节点v在时间步t的隐藏状态(即节点的表示)。∙xv是节点v的初始特征向量。∙N(v)是节点v的邻居节点集合。∙x(v,u)是边(v,u)的特征向量。f(⋅)和g(⋅)是可学习的映射函数,通常用神经网络来表示。\begin{aligned} &\text{RecGNNs的节点更新公式通常表示为:} \\ &h_{v}^{(t)}=f\left(x_{v},\sum_{u\in N(v)}g\left(h_{u}^{(t-1)},x_{(v,u)}\right)\right) \\ &\text{其中:} \\ &\bullet\quad h_v^{(t)}\text{ 是节点 }v\text{ 在时间步 }t\text{ 的隐藏状态(即节点的表示)。} \\ &\bullet\quad x_v\text{ 是节点 }v\text{ 的初始特征向量。} \\ &\bullet\quad N(v)\text{ 是节点 }v\text{ 的邻居节点集合。} \\ &\bullet\quad x_{(v,u)}\text{ 是边 }(v,u)\text{ 的特征向量。} \\ &\text{}f(\cdot)\text{ 和 }g(\cdot)\text{ 是可学习的映射函数,通常用神经网络来表示。} \end{aligned}

# 2. 卷积图神经网络（Convolutional Graph Neural Networks, ConvGNNs）

# 2.1 基本原理

  • ConvGNNs 将卷积操作从二维网格数据（如图像）推广到图数据。与传统卷积神经网络类似，ConvGNNs 也是通过聚合邻域信息来更新每个节点的特征表示。
  • ConvGNNs 与 RecGNNs 的主要区别在于，ConvGNNs 通常使用固定的卷积层数来进行操作，而不需要递归地传播信息直到平衡。

# 2.2 公式

一个典型的ConvGNN层的公式可以表示为:H(l+1)=σ(A~H(l)W(l))其中:∙H(l)是第l层的节点特征矩阵(大小为n×d)。∙A~=D−12(A+I)D−12是图的归一化邻接矩阵,其中A是邻接矩阵,I是单位矩阵,D是度矩阵。∙W(l)是第l层的权重矩阵。∙σ(⋅)是激活函数,例如ReLU。这个公式表示第l+1层的节点表示H(l+1)是通过将上一层的节点表示H(l)与归一化后的邻接矩阵A~和可学习的权重矩阵W(l)进行矩阵乘法,然后应用激活函数得到的。\begin{aligned} &\text{一个典型的ConvGNN层的公式可以表示为:} \\ &H^{(l+1)}=\sigma\left(\tilde{A}H^{(l)}W^{(l)}\right) \\ &\text{其中:} \\ &\bullet\quad H^{(l)}\text{ 是第 }l\text{ 层的节点特征矩阵(大小为 }n\times d\text{)。} \\ &\bullet\quad\tilde{A}=D^{-\frac12}\left(A+I\right)D^{-\frac12}\text{ 是图的归一化邻接矩阵,其中 }A\text{ 是邻接矩阵,}I\text{ 是} \\ &单位矩阵,D是度矩阵。 \\ &\begin{array}{cc}\bullet&W^{(l)}\text{ 是第 }l\text{ 层的权重矩阵。}\end{array} \\ &\bullet\quad\sigma(\cdot)\text{ 是激活函数,例如ReLU。} \\ &这个公式表示第 l+1 层的节点表示 H^{(l+1)} 是通过将上一层的节点表示 H^{(l)} 与 \\ &\text{归一化后的邻接矩阵 }\tilde{A}\text{ 和可学习的权重矩阵 }W^{(l)}\text{ 进行矩阵乘法,然后应用激活函} \\ &\text{数得到的。} \end{aligned}

# 2.3 具有多个图卷积层的 ConvGNN

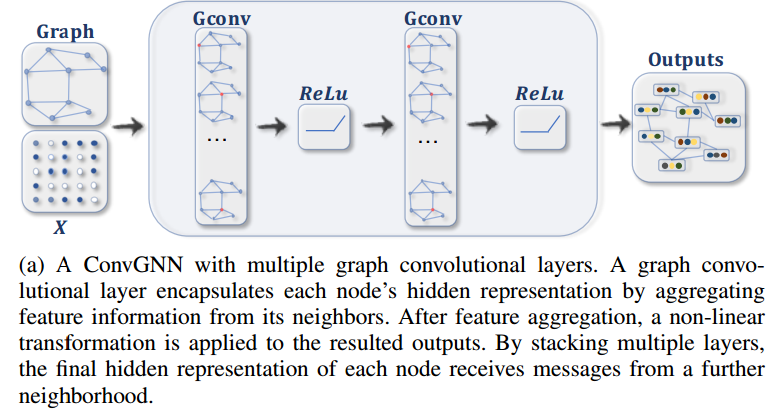
image.png

# 图的各部分解析：

  1. Graph (图)：

    • 图结构和特征矩阵 $ X $ 作为输入，图中的每个节点都由其特征向量表示。这些节点通过边相互连接，形成一个图结构。

  2. Graph Convolutional Layer (图卷积层，Gconv)：

    • 图卷积层的作用： 图卷积层对每个节点进行特征聚合（feature aggregation），即将节点的特征向量与其邻居节点的特征向量进行结合。这种聚合能够捕捉到节点的局部图结构信息。
    • 多层卷积： 图中展示了两个连续的图卷积层，每一层都对节点的特征进行聚合处理。第一层卷积聚合了节点的直接邻居的信息，第二层则进一步聚合了更远的邻居信息。

  3. ReLU (非线性激活函数)：

    • 在每个图卷积层之后，应用非线性激活函数 ReLU（Rectified Linear Unit），其作用是引入非线性，从而使得模型能够学习到更复杂的表示。这一步非常类似于传统神经网络中的激活函数作用。

  4. Outputs (输出)：

    • 经过多个图卷积层和激活函数的处理后，最终每个节点得到了其隐藏表示。这些表示包含了节点及其邻域的综合信息，是对输入节点特征的高层次表示。
    • 输出可以用于各种任务，比如节点分类、链接预测或图分类等。

# 工作流程总结：

  • 输入： 一个包含节点和边的图，以及每个节点的特征矩阵 $ X$。
  • 图卷积操作： 每个图卷积层对节点的特征进行聚合，并应用非线性激活函数（ReLU）。
  • 堆叠卷积层： 通过多个卷积层的堆叠，节点可以从更远的邻域中收集信息，从而获得更丰富的表示。
  • 输出： 最终输出的节点表示包含了每个节点从其邻居那里聚合来的信息，可以用于各种图分析任务。

# 2.4 具有池化和读出层的用于图分类的 ConvGNN

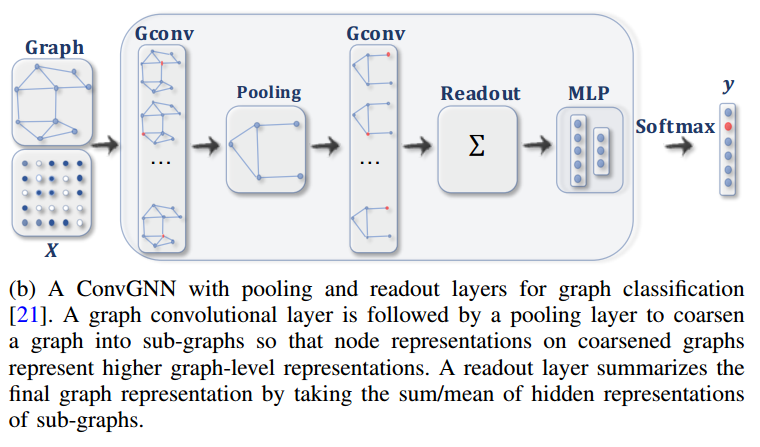
image.png

这张图展示了一个卷积图神经网络（Convolutional Graph Neural Network, ConvGNN）用于图分类任务的完整流程，包括图卷积层（Gconv）、池化层（Pooling）、读出层（Readout）和多层感知机（MLP），最终通过 Softmax 层输出分类结果。

# 图的各部分解析：

  1. Graph (图) 和 X (特征矩阵)：
    • 输入的图包含节点和边，节点具有特征矩阵 $ X$。这些特征将被传递到图卷积层中进行处理。
  2. Graph Convolutional Layers (图卷积层，Gconv)：
    • 这些层的作用是对每个节点的特征进行聚合，将邻居节点的特征信息汇总到当前节点中，从而更新节点的表示。
    • 在图中，两个图卷积层通过多次聚合操作，逐步提取更高层次的节点特征。
  3. Pooling Layer (池化层)：
    • 池化层用于对图进行简化（或称为图的 “粗化”），即将原始图中的节点聚合成较少的 “子图”。这样做的目的是减少图的规模，使得每个节点表示更高层次的图结构信息。
    • 经过池化操作，每个子图的节点表示将包含更多图的全局信息。
  4. Readout Layer (读出层)：
    • 读出层的作用是将所有节点的表示整合为一个全局的图表示。常见的整合方式包括对所有节点表示进行求和或取平均值。
    • 读出操作生成了一个代表整个图的向量，这个向量将作为分类器的输入。
  5. MLP (多层感知机) 和 Softmax：
    • 多层感知机（MLP）是一个全连接的神经网络层，用于对读出层生成的全局图表示进行进一步处理。
    • 最后一层是 Softmax 层，它将 MLP 的输出转换为各个类别的概率分布，最终输出图的分类结果 yy。

# 工作流程总结：

  • 输入： 包含节点和边的图，以及节点的特征矩阵 $ X$。
  • 图卷积层： 对节点特征进行聚合，提取局部和全局图结构信息。
  • 池化层： 将图简化为子图，进一步提取高层次表示。
  • 读出层： 整合所有节点的表示为全局图表示。
  • MLP 和 Softmax： 通过全连接网络和 Softmax 层对全局图表示进行分类，输出最终的分类结果。

# 基于频谱的卷积图神经网络（Spectral-based ConvGNNs）

image.png

image.png

image.png

# 3. 图自编码器（Graph Autoencoders, GAEs）

# 3.1 基本原理

  • 图自编码器是无监督学习模型，旨在将图的节点或整个图嵌入到一个低维的潜在空间中，然后通过解码器从该潜在表示中重建图结构。
  • GAEs 通常用于学习图的嵌入表示，这些嵌入可以用于下游任务（如分类、聚类等）。

# 3.2 公式

图自编码器的基本架构包括编码器和解码器两部分：

  1. 编码器： 编码器将图的特征嵌入到一个低维潜在空间中，常见的编码器形式为：Z=GNNEncoder(X,A)Z = \text{GNNEncoder}(X, A) 其中：

    • ZZ 是低维的潜在嵌入矩阵。
    • XX 是节点特征矩阵。
    • AA 是图的邻接矩阵。

  2. 解码器： 解码器试图从嵌入表示中重建图结构，常见的解码器形式为：A^=σ(ZZT)\hat{A} = \sigma(Z Z^T) 其中：

  • A^\hat{A} 是重建后的邻接矩阵。
  • ZTZ^T 是嵌入矩阵的转置。
  • σ(⋅)\sigma(\cdot) 是激活函数，如 sigmoid。

GAE 的目标是最小化原始图的邻接矩阵AA 与重建后的邻接矩阵 A^\hat{A} 之间的差异，这通常通过最小化重建损失来实现。

# 3.3 用于网络嵌入的 GAE

image.png

这张图展示了一个图自编码器（Graph Autoencoder, GAE）的工作流程，用于网络嵌入。GAE 的目标是将图嵌入到低维空间中，然后重构图的邻接矩阵，通过最小化实际邻接矩阵和重构邻接矩阵之间的差异来进行训练。

# 图的各部分解析：

  1. 输入 (A 和 X)：
    • A (邻接矩阵)： 输入图的邻接矩阵 $ A $ 表示图的结构信息，描述了图中节点之间的连接关系。
    • X (特征矩阵)： 输入图的节点特征矩阵 $ X $ 包含了每个节点的属性信息。这些信息将被传递到编码器中处理。
  2. Encoder (编码器)：
    • 编码器使用图卷积层（Gconv）来对每个节点进行特征聚合，从而生成节点的嵌入表示 ZZ。
    • 图卷积层逐层处理节点特征，将邻居节点的特征信息融合到当前节点的表示中，从而生成更具全局信息的节点嵌入。
  3. Z (节点嵌入)：
    • 编码器的输出是节点嵌入矩阵 ZZ，其中每个节点 v 对应一个嵌入向量 zvz_v。这些嵌入向量位于一个低维的潜在空间中，捕捉了图的结构和节点属性信息。
  4. Decoder (解码器)：
    • 解码器的任务是根据节点嵌入矩阵 $ Z $ 来重构图的邻接矩阵。
    • 重构过程： 解码器计算节点嵌入的两两距离（例如通过点积 ZZTZ Z^T），并通过一个非线性激活函数ϕ(⋅)\phi(\cdot) 来生成重构后的邻接矩阵A^\hat{A}。
  5. Output A^\hat{A}(重构的邻接矩阵)：
    • 输出的 A^\hat{A} 是根据节点嵌入重构的邻接矩阵。模型通过将 A^\hat{A} 与原始邻接矩阵 AA 进行比较，计算它们之间的差异并最小化这种差异，从而优化模型参数。
    • 这种优化过程使得节点的嵌入 ZZ 能够捕捉到图的结构信息。

# 工作流程总结：

  • 输入： 包含节点特征和邻接矩阵的图数据。
  • 编码器： 使用图卷积层对节点特征进行聚合，生成低维嵌入表示 ZZ。
  • 解码器： 根据节点嵌入 $ Z$ 重构邻接矩阵 A^\hat{A}，并通过最小化重构误差来训练模型。
  • 输出： 重构的邻接矩阵 A^\hat{A} 用于评估模型性能，节点嵌入 ZZ 可用于下游任务，如节点分类或图聚类。

# 4. 时空图神经网络（Spatial-Temporal Graph Neural Networks, STGNNs）

# 4.1 基本原理

  • STGNNs 专注于处理节点属性随时间动态变化的图结构，特别适用于需要同时考虑空间和时间依赖性的任务，如交通预测和动作识别。
  • STGNNs 通常结合图卷积和时间序列建模方法（如 RNN 或 CNN）来捕捉这些依赖性。

# 4.2 公式

一个简单的STGNN可以表示为:H(t+1)=RNN(GNN(H(t),A),H(t))其中:∙H(t)是时刻t的节点特征矩阵。∙A是图的邻接矩阵。∙GNN(⋅)表示图卷积操作,用于捕捉空间依赖性。∙RNN(⋅)表示递归神经网络操作,用于捕捉时间依赖性。习空间和时间上的相关性。\begin{aligned} &一个简单的STGNN可以表示为: \\ &H^{(t+1)}=\mathrm{RNN(GNN(}H^{(t)},A),H^{(t)}) \\ &其中: \\ &\bullet H^{(t)}\text{ 是时刻 }t\text{ 的节点特征矩阵。} \\ &\bullet A\text{ 是图的邻接矩阵。} \\ &\bullet\mathrm{~GNN}(\cdot)\text{ 表示图卷积操作,用于捕捉空间依赖性。} \\ &\bullet\mathrm{~RNN}(\cdot)\text{ 表示递归神经网络操作,用于捕捉时间依赖性。} \\ &习空间和时间上的相关性。 \end{aligned}

# 4.3 时空图预测的 STGNN

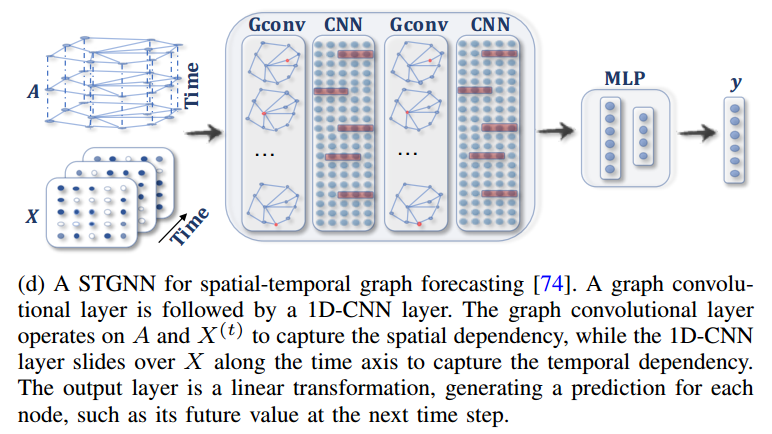
image.png

这张图展示了时空图神经网络（Spatial-Temporal Graph Neural Network, STGNN）的工作流程，该模型用于处理具有时空依赖性的图数据。STGNN 将图卷积（Graph Convolution, Gconv）和卷积神经网络（Convolutional Neural Network, CNN）结合在一起，用于捕捉图结构中的空间依赖性和时间维度上的动态变化。

# 图的各部分解析：

  1. 输入 (A 和 X)：
    • A (邻接矩阵随时间变化)： 输入图的邻接矩阵 AA 是随时间变化的，表示图结构在不同时间点的连接关系。这种动态邻接矩阵捕捉了节点之间的时空依赖性。
    • X (特征矩阵随时间变化)： 输入的节点特征矩阵 $ X$ 也是随时间变化的，表示每个节点在不同时间点的属性。这反映了节点特征随时间的动态变化。
  2. Graph Convolutional Layer (图卷积层，Gconv)：
    • 图卷积层用于提取图结构中的空间依赖性。每一层图卷积操作都会将邻居节点的特征信息聚合到当前节点中，更新节点的表示。
    • 图中展示了多个图卷积层，逐层提取节点的空间信息。
  3. Convolutional Neural Network Layer (CNN)：
    • 卷积神经网络层用于捕捉节点特征的时间依赖性。通过在时间维度上应用卷积操作，CNN 能够提取节点特征随时间变化的模式。
    • 图中展示了多个 CNN 层，与图卷积层交替使用，以同时捕捉空间和时间依赖性。
  4. MLP (多层感知机)：
    • 在通过多个图卷积层和 CNN 层提取了时空特征后，使用多层感知机（MLP）进一步处理这些特征，并生成最终的输出表示。
  5. Output yy (输出)：
    • 最后的输出 $ y$ 通常是一个分类或回归的结果，用于预测图中的节点或整个图的某种属性。例如，可能是对节点的分类、图的预测或时间序列的回归任务。

# 工作流程总结：

  • 输入： 动态图的邻接矩阵 $ A和节点特征矩阵和节点特征矩阵 X$，它们都随时间变化。
  • 图卷积层： 提取图结构中的空间依赖性信息。
  • CNN 层： 提取节点特征的时间依赖性信息。
  • 多层感知机： 对时空特征进行进一步处理，生成最终的分类或回归结果。
  • 输出： 预测图的某种属性或节点的某种状态。

# 扩散卷积神经网络 (Diffusion Convolutional Neural Network, DCNN)

image.png