Home deep-learning

# 如何实现多分类问题？

# 概率分布

  • 每个可能的输出概率都需要大于等于零
  • 所有可能分类概率之和为 1

# 函数区别

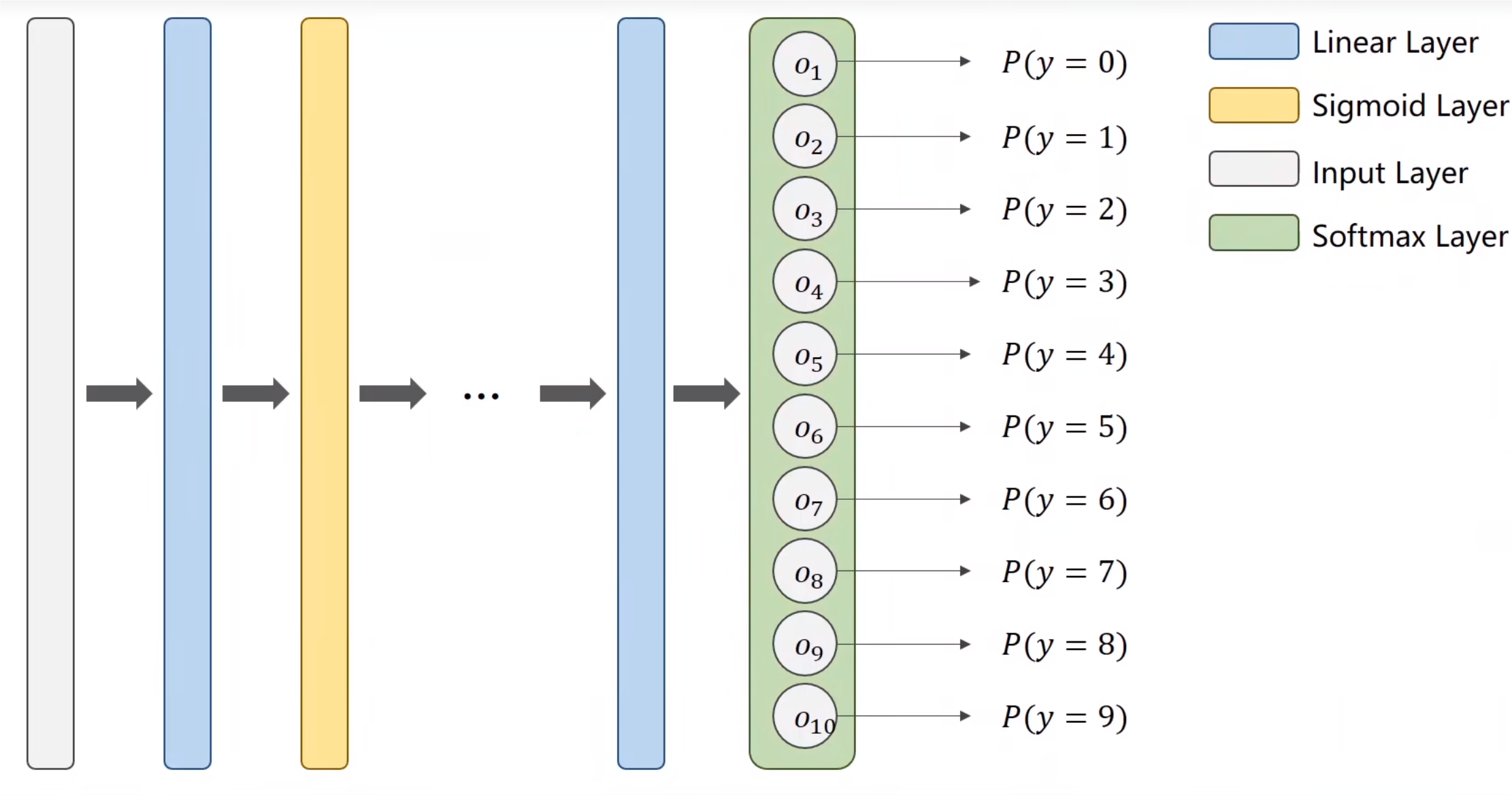
QQ_1722164470310.png

  • 中间处理过程可以用 Sigmoid 函数
  • 最终层应该为 Softmax 层

# Softmax 实现

QQ_1722190799779.png

# One-hot 方法

One-hot 编码是一种将分类数据转换为二进制向量的方法，通常用于将离散的分类标签转换为机器学习算法可以处理的格式。每个类别用一个独特的二进制向量表示，其中只有一个位置的值为 1，其余位置的值为 0。这样做的好处是可以将分类数据转化为数值数据，方便模型处理。

# 损失函数求法

Loss(Y^,Y)=−Ylog⁡Y^Loss(\widehat{Y},Y)=-Y{\log\widehat{Y}}

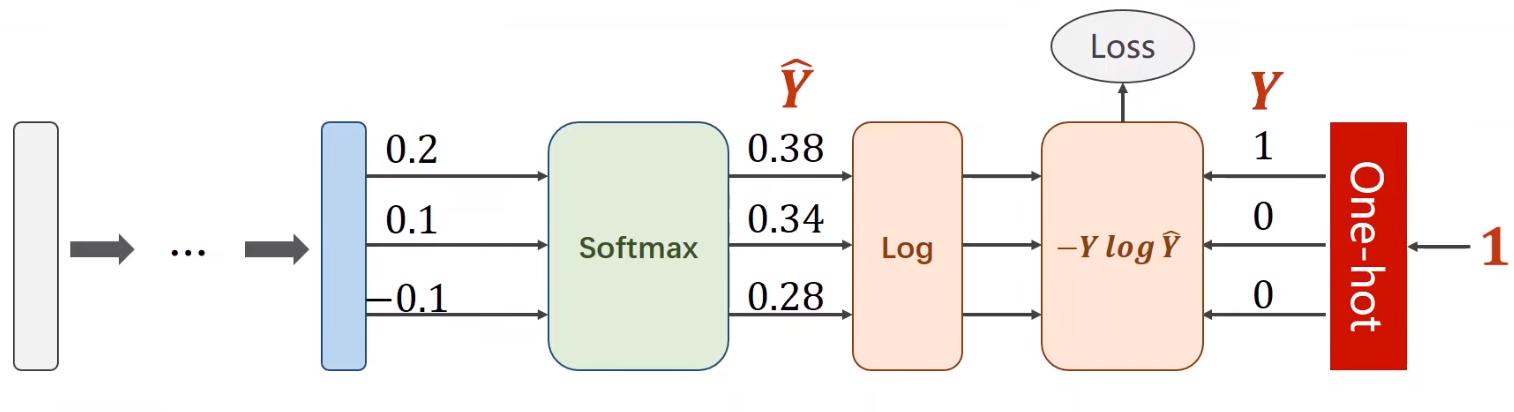
QQ_1722165173590.png

# 代码实现

# numpy 格式

1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np

# 定义真实标签和预测分数
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])

# 计算预测概率（Softmax）
y_pred = np.exp(z) / np.exp(z).sum()

# 计算交叉熵损失
loss = (-y * np.log(y_pred)).sum()

print(loss)

# torch 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch

# 定义真实标签和预测分数
y = torch.LongTensor([0])
z = torch.Tensor([[0.2, 0.1, -0.1]])

# 定义交叉熵损失函数
criterion = torch.nn.CrossEntropyLoss()

# 计算损失
loss = criterion(z, y)

print(loss)

  • 输出的最后一层不要进行激活 —— 即最后一层输出不要进行非线性变换
  • 损失函数用 CrossEntropyLoss() 库实现

# 多分类问题代码

# 引用相关库

1
2
3
4
5
6
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# 数据处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
batch_size = 64

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

train_dataset = datasets.MNIST(
    root='../dataset/mnist/',
    train=True,
    download=True,
    transform=transform
)

train_loader = DataLoader(
    train_dataset,
    shuffle=True,
    batch_size=batch_size
)

test_dataset = datasets.MNIST(
    root='../dataset/mnist/',
    train=False,
    download=True,
    transform=transform
)

test_loader = DataLoader(
    test_dataset,
    shuffle=False,
    batch_size=batch_size
)

  • transforms.ToTensor() : 这个操作将图像从 PIL 图像或者 numpy 数组转换为 PyTorch 张量（Tensor）。在转换过程中，它还会将图像的像素值从 0-255 缩放到 0-1 之间。这个步骤是必要的，因为 PyTorch 模型需要张量格式的数据作为输入。
  • transforms.Normalize((0.1307,), (0.3081,)) : 这个操作对图像进行标准化处理。标准化是通过减去均值并除以标准差来完成的，这样可以使数据具有零均值和单位方差。对于 MNIST 数据集，经验上得出的像素值均值为 0.1307，标准差为 0.3081。这个步骤可以加速模型的训练收敛，并提高模型的泛化能力。
  • W:长、H:宽、C：通道W:长、H:宽、C：通道 pytorch 中将W×H×XW×H×X 转为C×W×HC×W×H，以便高效运算。
  • 故此处的 transform 将Z28×28,ріхеl∈{0,...,255}\mathbb{Z}^{28\times28},\text{ріхе}l\in\{0,...,255\} 转换为R1×28×28,pixle∈[0,1]\mathbb{R}^{1\times28\times28},pixle\in[0,1]. 其中1×28×28分别为C×W×H1×28×28分别为C×W×H。
  • 数据标准化：Pixel_{norm}=\frac{Pixel_{origin}-mean}

# 用 relu 库来预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = nn.Linear(784, 512)
        self.l2 = nn.Linear(512, 256)
        self.l3 = nn.Linear(256, 128)
        self.l4 = nn.Linear(128, 64)
        self.l5 = nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        x = self.l5(x)
        return x

model = Net()

criterion=torch.nn.CrossEntropyLoss()	#交叉熵损失
optimizer=optim.SGD(model.parameters(),lr=0.01,momentum=0.5) #

# Example usage:
# print(model)
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        # forward + backward + update
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))

if __name__=='__main__':
    for epoch in range(10):
        train(epoch)
        test()

  • 在优化器中， momentum 是一个加速梯度下降过程的技术。具体来说， momentum 是用来减少训练过程中震荡的一种方法，可以加快收敛速度。

  • 详细解释

    在梯度下降中，更新权重的公式通常是：

    w=w−η⋅∇J(w)w = w - \eta \cdot \nabla J(w)

    其中：

    • ww 是权重。
    • η\eta 是学习率。
    • ∇J(w\nabla J(w) 是损失函数对权重的梯度。

    引入动量后，权重的更新公式变为：

    vt=γ⋅vt−1+η⋅∇J(wt)v_t = \gamma \cdot v_{t-1} + \eta \cdot \nabla J(w_t)

    wt+1=wt−vtw_{t+1}=w_t-v_t

    其中：

    • 是第 tt 次更新时的动量项。
    • γ\gamma 是动量系数（通常在 0 到 1 之间，图中为 0.5）。
    • vt−1v_{t-1} 是前一次更新时的动量项。

    动量的引入使得每次更新不仅依赖当前的梯度，还会考虑前一次更新的方向，从而能够平滑梯度更新的路径，减少梯度下降过程中的震荡。动量项在梯度方向保持一致时，会加快收敛速度，而在梯度方向发生变化时，会起到抑制作用，从而使得更新更加平滑。

  • relu 函数：

    ReLU(x)=max⁡(0,x)\mathrm{ReLU}(x)=\max(0,x)

# 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.nn as nn
import torch.optim as optim

batch_size = 64

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

train_dataset = datasets.MNIST(
    root='../dataset/mnist/',
    train=True,
    download=True,
    transform=transform
)

train_loader = DataLoader(
    train_dataset,
    shuffle=True,
    batch_size=batch_size
)

test_dataset = datasets.MNIST(
    root='../dataset/mnist/',
    train=False,
    download=True,
    transform=transform
)

test_loader = DataLoader(
    test_dataset,
    shuffle=False,
    batch_size=batch_size
)
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = nn.Linear(784, 512)
        self.l2 = nn.Linear(512, 256)
        self.l3 = nn.Linear(256, 128)
        self.l4 = nn.Linear(128, 64)
        self.l5 = nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        x = self.l5(x)
        return x

model = Net()

criterion=torch.nn.CrossEntropyLoss()	#交叉熵损失
optimizer=optim.SGD(model.parameters(),lr=0.01,momentum=0.5) #

# Example usage:
# print(model)
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        # forward + backward + update
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))

if __name__=='__main__':
    for epoch in range(10):
        train(epoch)
        test()

  • x = x.view(-1, 784) ：将输入的图像展平成大小为 (-1, 784) 的二维张量（-1 表示自动计算维度大小）。
  • x = F.relu(self.l1(x)) ：将输入传递给第一层，并应用 ReLU 激活函数。
  • x = self.l5(x) ：将第四层的输出传递给第五层（没有激活函数，因为这是最终输出层）。
  • 创建一个 Net 类的实例，即初始化神经网络模型。
  • 定义损失函数为交叉熵损失，用于多分类任务。
  • 定义优化器为随机梯度下降（SGD），学习率为 0.01，动量为 0.5。
  • running_loss = 0.0 ：初始化累积损失为 0。
  • for batch_idx, data in enumerate(train_loader, 0) ：遍历训练数据加载器。
  • inputs, target = data ：将数据分为输入 inputs 和目标 target 。
  • optimizer.zero_grad() ：清除优化器的梯度。
  • outputs = model(inputs) ：将输入传入模型，得到输出 outputs 。
  • loss = criterion(outputs, target) ：计算损失。
  • loss.backward() ：反向传播，计算梯度。
  • optimizer.step() ：更新模型参数。
  • running_loss += loss.item() ：累加损失。
  • if batch_idx % 300 == 299 ：每 300 个批次打印一次平均损失。
  • print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300)) ：打印当前轮次和批次的平均损失。
  • running_loss = 0.0 ：重置累积损失。