Home deep-learning

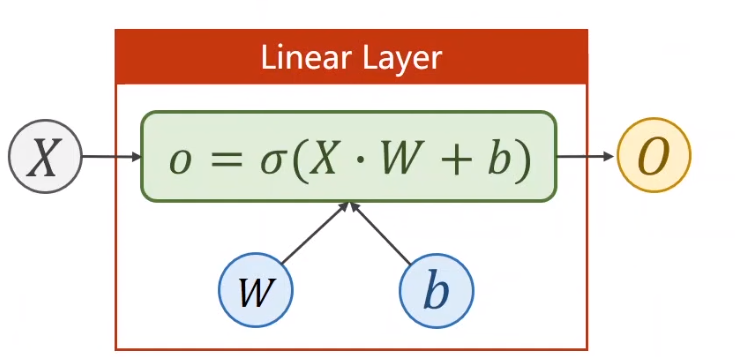
# 多维特征输入

# 激活函数变化

y^(i)=σ(∑n=18xn(i)⋅ωn+b)\widehat{y}^{(i)}=\sigma(\sum_{n=1}^{8}{x_{n}^{(i)}}\cdot{\omega_{n}}+b)

即为：

∑n=18xn(i)⋅ωn=[x1(i)⋯x8(i)][ω1⋮ω8]\sum_{n=1}^8x_n^{(i)}\cdot\omega_n=\begin{bmatrix}x_1^{(i)}&\cdots&x_8^{(i)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}

故完整的多维特征输入公式为:

y^(i)=σ([x1(i)⋯x8(i)][ω1⋮ω8]+b)=σ(z(i))\begin{aligned}\hat{y}^{(i)}&=\sigma(\begin{bmatrix}x_1^{(i)}&\cdots&x_8^{(i)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}+b)\\&=\sigma(z^{(i)})\end{aligned}

对其进行多层递进，递进公式如下：

[y^(1)⋮y^(N)]=[σ(z(1))⋮σ(z(N))]=σ([z(1)⋮z(N)])\begin{bmatrix}\hat{y}^{(1)}\\\vdots\\\hat{y}^{(N)}\end{bmatrix}=\begin{bmatrix}\sigma(z^{(1)})\\\vdots\\\sigma(z^{(N)})\end{bmatrix}=\sigma(\begin{bmatrix}z^{(1)}\\\vdots\\z^{(N)}\end{bmatrix})

z(1)=[x1(1)⋯x8(1)][ω1⋮ω8]+b⋮z(N)=[x1(N)⋯x8(N)][ω1⋮ω8]+bz^{(1)}=\begin{bmatrix}x_1^{(1)}&\cdots&x_8^{(1)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}+b\\\vdots\\z^{(N)}=\begin{bmatrix}x_1^{(N)}&\cdots&x_8^{(N)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}+b

上式等价于：

[z(1)⋮z(N)]=[x1(1)...x8(1)⋮⋱⋮x1(N)...x8(N)][ω1⋮ω8]+[b⋮b]\begin{bmatrix}z^{(1)}\\\vdots\\z^{(N)}\end{bmatrix}=\begin{bmatrix}x_1^{(1)}&...&x_8^{(1)}\\\vdots&\ddots&\vdots\\x_1^{(N)}&...&x_8^{(N)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}+\begin{bmatrix}b\\\vdots\\b\end{bmatrix}

# 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import torch.nn as nn

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear = nn.Linear(8, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear(x))
        return x

model = Model()

  • nn.Linear(8, 1) ，输入维度为 8，输出维度为 1

  • QQ_1722103042500.png

  • 也可以先用 Linear(8,2) 转为 2 维，然后再 Linear(2,1) 转为 1 维。分布降低，为了保证非线性，每次调整后都加入非线性激活函数σ()\sigma()

  • 学习能力不要太强 —— 学习能力过强会将噪声的规律也学习到，导致过拟合！所以还原最真实的状态最重要，即具有泛化能力。

  • 多层学习代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    import torch
    import torch.nn as nn

    class Model(nn.Module):
        def __init__(self):
            super(Model, self).__init__()
            self.linear1 = nn.Linear(8, 6)
            self.linear2 = nn.Linear(6, 4)
            self.linear3 = nn.Linear(4, 1)
            self.sigmoid = nn.Sigmoid()

        def forward(self, x):
            x = self.sigmoid(self.linear1(x))
            x = self.sigmoid(self.linear2(x))
            x = self.sigmoid(self.linear3(x))
            return x

    model = Model()

# 设计思路

QQ_1722104183902.png

# 具体算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import numpy as np
import torch
import torch.nn as nn

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8, 6)
        self.linear2 = nn.Linear(6, 4)
        self.linear3 = nn.Linear(4, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

for epoch in range(100):
    # Forward
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    # Backward
    optimizer.zero_grad()
    loss.backward()

    # Update
    optimizer.step()

  • 分隔符为 ,
  • xy[:,:-1] ：最后一列舍去
  • xy[:,[-1]] ：最终拿出来的是矩阵
  • criterion ：损失函数
  • optimizer ：优化器
  • 不同激活函数如下：
    QQ_1722104488489.png

# Batch 的作用

# 定义

Batch 是指在一次迭代中使用的一组训练样本。在神经网络训练过程中，数据集通常被分成多个批次（Batch），每个批次会独立进行前向传播和后向传播，并更新模型参数。

# 作用

  • 提高计算效率：批处理使得计算过程可以并行化，在 GPU 等硬件上能够显著提升计算速度。
  • 稳定梯度：通过在批次内的样本上计算平均梯度，可以减少梯度更新的波动，从而使训练更加稳定。
  • 内存优化：将大数据集分成小批次处理，可以有效减少内存占用，适应更多样本的数据集训练。

# 训练过程中的 Batch 处理

  • Epoch：一个 Epoch 表示整个训练数据集被完整地传递通过神经网络一次。一个 Epoch 包含多个批次。
  • Mini-Batch Gradient Descent：实际训练中最常用的方法，将数据分成多个小批次，通过这些小批次逐步更新模型参数。
  • Batch Gradient Descent：使用整个数据集计算梯度并更新模型参数，适用于数据集较小的情况。
  • 随机梯度下降（SGD）：每次使用一个样本更新模型参数，适用于数据集较大时但通常会导致梯度不稳定。

# Batch Size 的选择

  • 小 Batch Size（如 32 或 64）：训练过程中会产生更多的噪声，收敛更快但波动较大。
  • 大 Batch Size（如 256 或更大）：训练更稳定，但计算需求和内存需求较高。
  • 一般建议从小 Batch Size 开始，根据需要和硬件能力调整。

# 噪声

在深度学习和机器学习中，噪声（Noise）通常指的是数据中不相关、随机或误导性的信息，这些信息可能会干扰模型的训练过程，从而影响模型的性能。噪声可以来源于多个方面，包括数据采集过程中的误差、不相关的特征、标签错误等。以下是关于噪声的详细介绍：

# 噪声对模型的影响

  1. 过拟合：
    • 噪声可能导致模型过拟合训练数据，即模型过于拟合数据中的噪声，导致泛化能力下降。
    • 过拟合模型在训练集上的表现很好，但在测试集上的表现较差。
  2. 模型性能下降：
    • 噪声会干扰模型的学习过程，导致模型在训练过程中无法准确捕捉数据中的模式，从而影响模型性能。
  3. 训练不稳定：
    • 数据中的噪声会引起梯度计算的波动，使训练过程不稳定，训练时间延长。

# 示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset

# 生成一些示例数据
# 假设我们有1000个样本，每个样本有10个特征，目标是一个标量
X = torch.randn(1000, 10)
y = torch.randn(1000, 1)

# 创建数据集和数据加载器
dataset = TensorDataset(X, y)
batch_size = 32
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

# 定义简单的线性模型
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.linear = nn.Linear(10, 1)
    
    def forward(self, x):
        return self.linear(x)

model = SimpleModel()

# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 训练模型
num_epochs = 10
for epoch in range(num_epochs):
    for batch_X, batch_y in dataloader:
        # 前向传播
        outputs = model(batch_X)
        loss = criterion(outputs, batch_y)
        
        # 后向传播和优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

print("训练完成")

# 加载数据集

# 概念介绍

# 1. Epoch

定义：

  • 一个 Epoch 表示使用整个训练数据集进行一次前向传播和一次后向传播。

详细说明：

  • 在深度学习训练过程中，一个 Epoch 意味着模型已经看过了一次完整的数据集。
  • 训练通常需要多个 Epoch，以确保模型充分学习数据中的模式。
  • 每个 Epoch 结束后，模型参数会更新一次。

# 2. Batch Size

定义：

  • Batch Size 是指在一次前向和后向传播中使用的训练样本数量。

详细说明：

  • 将数据集分成多个小批次，每个小批次包含 Batch Size 数量的样本。
  • 使用较大的 Batch Size 可以提高计算效率，利用硬件（如 GPU）的并行计算能力。
  • 但较大的 Batch Size 需要更多的内存，并且可能导致训练模型的泛化能力下降。

# 3. Iteration（迭代数量）

定义：

  • Iteration 是指一次使用 Batch Size 数量的样本进行前向和后向传播的过程。一个 Epoch 包含多次 Iteration。

详细说明：

  • Iteration 的次数等于数据集样本数量除以 Batch Size。
  • 每次 Iteration 会使用一个 Batch 的数据进行模型参数更新。
  • 训练过程中，Iteration 的数量决定了模型参数更新的频率。

# 使用 mini-batch 的概念

1
2
3
4
# Training cycle
for epoch in range(training_epochs):
    # Loop over all batches
    for i in range(total_batch):

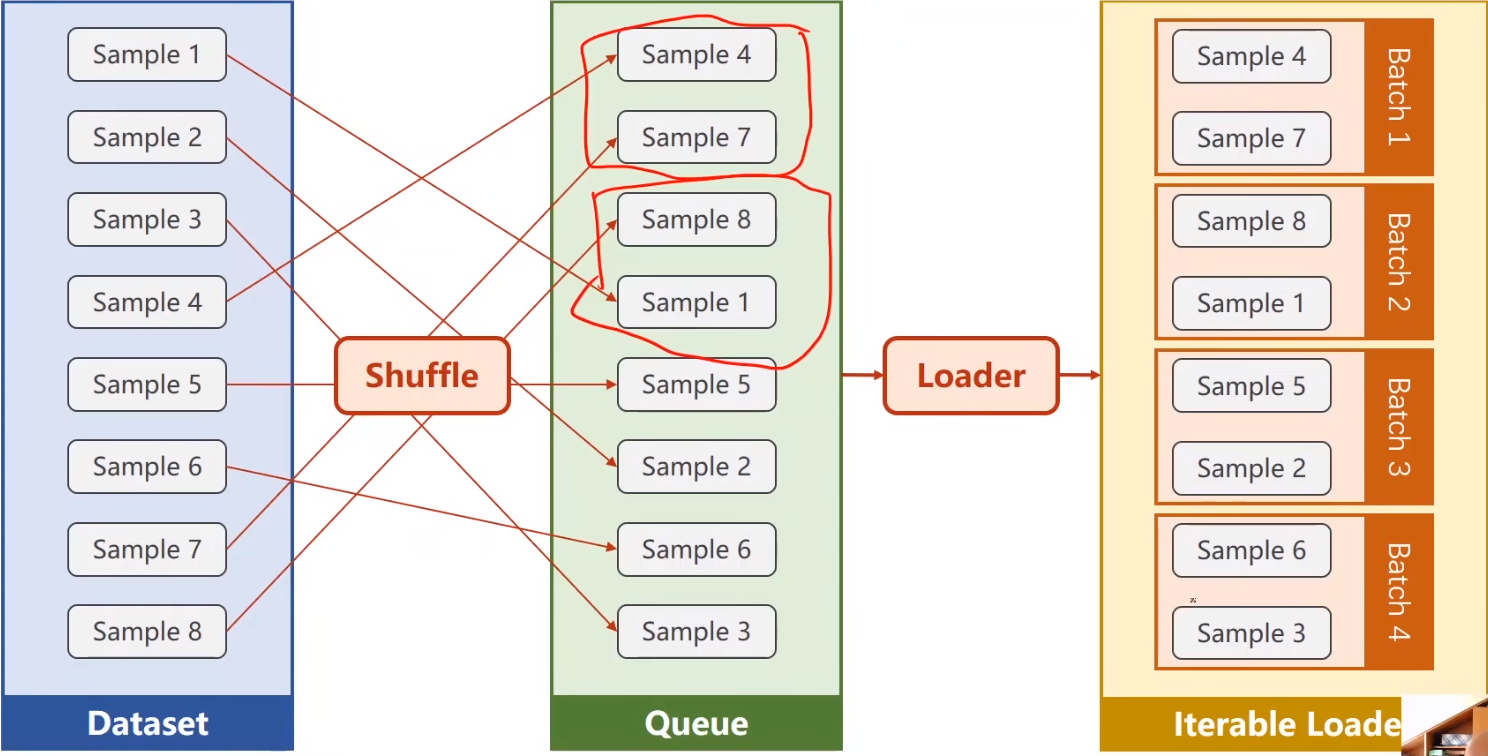
# DataLoader

DataLoader 是 PyTorch 中的一个类，用于将数据集封装起来，并提供批处理、打乱、并行加载等功能。它能够方便地加载数据进行模型训练和评估。

1
DataLoader: batch_size=2, shuffle=True

  • batch_size 参数指定每个 Batch 中包含的数据样本数量。在这个例子中， batch_size 设为 2，这意味着每次迭代中，DataLoader 会返回 2 个样本的 Batch。
  • shuffle 参数指定在每个 Epoch 开始前是否打乱数据顺序。在这个例子中， shuffle 设为 True，这意味着每个 Epoch 开始前，DataLoader 会将数据集中的样本顺序随机打乱。
    QQ_1722159140954.png

# 如何定义数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import torch
from torch.utils.data import Dataset, DataLoader

# 自定义数据集类
class DiabetesDataset(Dataset):
    def __init__(self):
        # 初始化数据集，这里假设我们有一些数据已经加载到self.data和self.labels中
        self.data = torch.randn(100, 10)  # 100个样本，每个样本10个特征
        self.labels = torch.randn(100, 1) # 100个样本，每个样本1个标签
    
    def __getitem__(self, index):
        # 获取指定索引的样本和标签
        return self.data[index], self.labels[index]
    
    def __len__(self):
        # 返回数据集的大小
        return len(self.data)

# 创建数据集实例
dataset = DiabetesDataset()

# 创建数据加载器
train_loader = DataLoader(dataset=dataset, # 数据集
                          batch_size=32, # batch的大小
                          shuffle=True, # 是否要打乱
                          num_workers=2) # 几个并行线程

# 测试数据加载器
for epoch in range(100):
    for i,data in enumerate(train_loader,0):
        ......

  • 如果报错，就将 loader 封装就行

  • 改写为

    1
    2
    3
    4
    if __name__=='__main__':
        for epoch in range(100):
            for i,data in enumerate(train_loader,0):
                .....

# 最终代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import torch
from torch.utils.data import Dataset, DataLoader
import numpy as np

class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :-1])  # 特征
        self.y_data = torch.from_numpy(xy[:, [-1]])  # 标签
    
    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]
    
    def __len__(self):
        return self.len

# 创建数据集实例
dataset = DiabetesDataset('diabetes.csv.gz')

# 创建数据加载器
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)

# 定义简单的模型、损失函数和优化器
model = torch.nn.Linear(10, 1)  # 假设有10个输入特征
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 训练模型
for epoch in range(100):
    for i, data in enumerate(train_loader, 0):
        # 1. 准备数据
        inputs, labels = data
        
        # 2. 前向传播
        y_pred = model(inputs)
        loss = criterion(y_pred, labels)
        print(epoch, i, loss.item())
        
        # 3. 后向传播
        optimizer.zero_grad()
        loss.backward()
        
        # 4. 更新参数
        optimizer.step()

# 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import torch
from torch.utils.data import Dataset, DataLoader

class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
    
    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]
    
    def __len__(self):
        return self.len

dataset = DiabetesDataset('diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()
    
    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(100):
    for i, data in enumerate(train_loader, 0):
        # 1. Prepare data
        inputs, labels = data
        # 2. Forward
        y_pred = model(inputs)
        loss = criterion(y_pred, labels)
        print(epoch, i, loss.item())
        # 3. Backward
        optimizer.zero_grad()
        loss.backward()
        # 4. Update
        optimizer.step()

# minist 代码判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import torch
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision import datasets

# 定义数据转换
transform = transforms.Compose([transforms.ToTensor()])

# 加载训练和测试数据集
train_dataset = datasets.MNIST(root='../dataset/mnist', train=True, transform=transform, download=True)
test_dataset = datasets.MNIST(root='../dataset/mnist', train=False, transform=transform, download=True)

# 创建数据加载器
train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=32, shuffle=False)

# 训练过程的示例
for batch_idx, (inputs, target) in enumerate(train_loader):
    # 在这里实现训练步骤
    # 例如，前向传播、计算损失、后向传播和参数更新等
    pass