# 矩阵求导的书

matrix.cookbook

# 线性模型

分为训练集$(x,y)$ 和测试集$(x,?)$

# 损失函数

$$loss=(\hat{y}-y)^2=(x*\omega-y)^2$$

# Mean Square Error 平均平方误差

$$cost=\frac1N\sum_{n=1}^N(\hat{\hat{y}}_n-y_n)^2$$

# 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

def forward(x):
    return x * w

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
    print('w=', w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val, y_val)
        l_sum += loss_val #损失函数求和
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3) # 转成MSE
    w_list.append(w)
    mse_list.append(l_sum / 3)

# 梯度下降法

$$梯度：\frac{\partial cost}{\partial\omega}$$

根据梯度的变化来灵活调整学习率:

$$\underline{\omega}=\underline{\omega}-\underline{\alpha}\frac{\partial cost}{\partial\omega}$$

但是这样只能找到局部最优，找不到全局最优

鞍点：梯度等于零

# 梯度下降发应用于损失函数

$$\begin{aligned} \frac{\partial cost(\omega)}{\partial\omega}& =\frac\partial{\partial\omega}\frac1N\sum_{n=1}^N(x_n\cdot\omega-y_n)^2 \\ &=\frac1N\sum_{n=1}^N\frac\partial{\partial\omega}(x_n\cdot\omega-y_n)^2 \\ &=\frac{1}{N}\sum_{n=1}^{N}2\cdot(x_{n}\cdot\omega-y_{n})\frac{\partial(x_{n}\cdot\omega-y_{n})}{\partial\omega} \\ &=\frac1N\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n) \end{aligned}$$

# 对于前文函数的梯度下降算法

$$\omega=\omega-\alpha\frac1N\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)$$

# 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print('Predict (before training)', 4, forward(4))
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= 0.01 * grad_val
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('Predict (after training)', 4, forward(4))

• w 是线性模型的初始权重
• cost(xs,ys) 是损失函数
• gradients 梯度函数：先把$\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)$ 计算出来，最终返回 $ \frac {1}{N}\sum_{n=1}^N2\cdot x_n\cdot (x_n\cdot\omega-y_n)$
• 将$\frac1N\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)$ 以 grad_val = gradient(x_data, y_data) 表示
• 最后进行训练迭代

# 随机梯度下降

$$\omega=\omega-\alpha\frac{\partial loss}{\partial\omega}$$

拿单个样本的损失函数对权重求导然后更新 —— 更加灵活。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

def gradient(x, y):
    return 2 * x * (x * w - y)

print('Predict (before training)', 4, forward(4))

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        grad = gradient(x, y)
        w -= 0.01 * grad
        print('\tgrad: ', x, y, grad)
    l = loss(x, y)
    print('progress:', epoch, "w=", w, "loss=", l)

print('Predict (after training)', 4, forward(4))

• 直接用单个损失函数来计算。

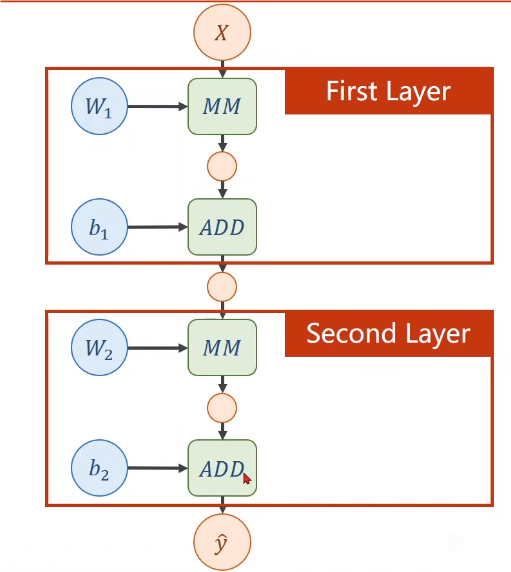
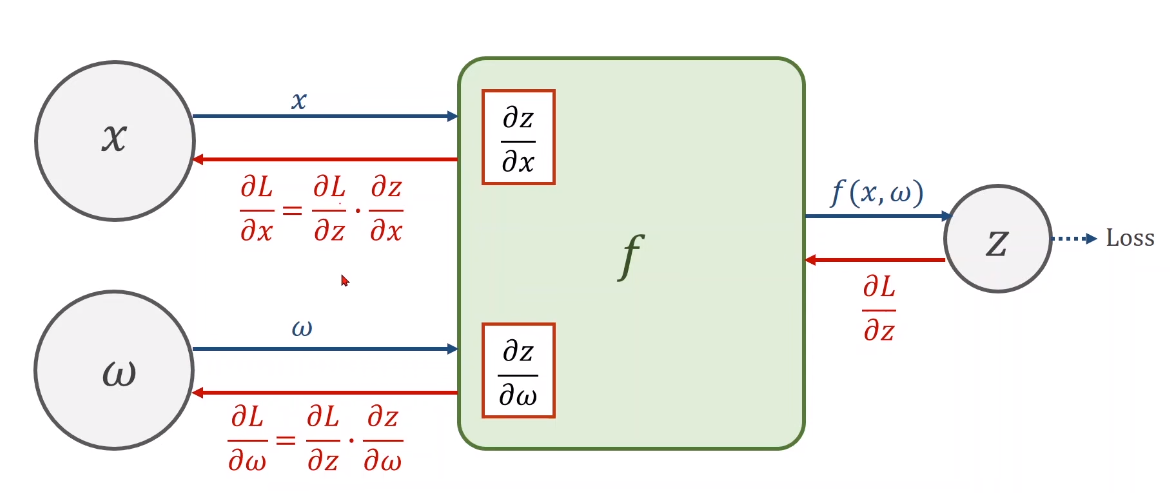
# 反向传播

• 先将 x 以权重 w 进行预测得到$\hat y$
• 通过$\omega=\omega-\alpha\frac{\partial loss}{\partial\omega}$ 来更新$\omega$
• $\hat{y}=W_2(W_1\cdot X+b_1)+b_2$
• 隐藏层：$W_1 \cdot X+b_1$
• 激活函数$\sigma()$: 对每一层加一个非线性函数 —— 增加复杂程度。
  正因为激活函数，使得深度有了变化，学习效果也就不断提升。
• 反向传播：
  反向传播 —— 更新参数$\omega$

# Pytorch 讲解

# Tensor——PyTorch 重要元素

• 保持元素 (Data：$\omega$) 和梯度 (Grad:$\frac{\partial loss}{\partial\omega}$)

# 代码实现

1
2
3
4
5
6
7

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = torch.Tensor([1.0])
w.requires_grad = True

• w.requires_grad = True ：表示模型需要计算梯度。

1
2
3
4
5
6

def forward(x):
    return x * w

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

• w : 是一个 tensor
• forward : 计算$\hat y$
• loss ：损失函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14

print("predict (before training)", 4, forward(4).item())

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data
        
        w.grad.data.zero_()
    
    print("progress:", epoch, l.item())

print("predict (after training)", 4, forward(4).item())

• loss ：计算损失函数
• l : 损失函数
• l.backward() : 计算链路上的所有需要的梯度，并且存到变量里面。
• w.data = w.data - 0.01 * w.grad.data : 因为 w 是一个 tensor ，为了计算具体的数值，需要操作到 w.grad.data
• w.grad.data.zero_() ：将权重里计算好的梯度等全部清零。

# 用 pytorch 实现线性回归

在 pytorch 中，如果计算$\hat y=\omega \cdot x+b$，当$x$ 为$3×1$ 矩阵时，$\omega 和 b$ 也会自动扩充为$3×1$ 的矩阵

# torch.nn.Linear

torch.nn.Linear 类对输入数据应用线性变换。这种变换可以用以下方程表示：

$$y=Ax+b$$

# 参数

• in_features: 每个输入样本的特征数量（输入特征的维度）。
• out_features: 每个输出样本的特征数量（输出特征的维度）。
• bias: 如果设置为 False ，该层将不会学习一个加性的偏置。默认值是 True 。

# 形状

• 输入: $(N, *, \text{in\_features})$`，其中 $*$ 表示任何数量的附加维度。例如，对于形状为 $(N, \text{in\_features})$ 的二维输入，$N$ 是批量大小，$\text{in\_features}$ 是输入特征的数量。
• 输出😒 (N, *, \text{out_features})$，其中除了最后一维，其他维度与输入形状相同。对于形状为$ (N, \text {out_features})$ 的二维输出，$N$ 是批量大小，$\text{out\_features}$ 是输出特征的数量。

# 变量

• weight: 模型中可学习的权重，其形状为 。
• bias: 模型中可学习的偏置，其形状为$(\text{out\_features})$。

在一个简单的线性层中，输入特征通过一个学习到的权重矩阵和一个可选的偏置向量被转换为输出特征，这使得模型能够学习输入和输出之间的关系。这种变换在神经网络中对于回归和分类等任务是至关重要的。

# 自己设计可调用类

1
2
3
4
5
6
7
8
9
10
11
12

# 定义一个可调用的类
class sky:
    def __init__(self):
        pass

    def __call__(self, *args, **kwargs):
		pass
    
def func(a,b,c,x,y):   #升级版：def func(*args,x,y) 这样可以不限制前面的数量
    pass			   #超级升级版:def func(*args,**kwargs) 这样可以不限制参数输入的数量 

func(1,2,4,3,x=3,y=5)

• *args 用于将不定数量的位置参数传递给函数。位置参数是指那些按顺序传递的参数。
• 在函数内部， *args 是一个元组，包含了所有传递给函数的额外位置参数。
• **kwargs 用于将不定数量的关键字参数传递给函数。关键字参数是指那些以 key=value 形式传递的参数。
• 在函数内部， **kwargs 是一个字典，包含了所有传递给函数的额外关键字参数。

# 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import torch
import torch.nn as nn  

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])

class LinearModel(nn.Module):
    def __init__(self): #构造函数
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x): #前馈转播
        y_pred = self.linear(x)
        return y_pred

model = LinearModel()

criterion = torch.nn.MSELoss(size_average=False) #MES：损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(100):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # Output weight and bias
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

# Test Model
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

• nn :Neural Network

• LinearModel() : 可以直接调用的线性模型

• torch.nn.MSELoss(size_average=False) : 继承自 nn ， size_average=False : 不求均值

• torch.optim.SGD : 优化器，

• model.parameters() 返回模型中所有需要优化的参数，这些参数将由优化器在训练过程中进行更新。

• lr=0.01 : 指定了学习率（learning rate）。学习率是一个控制参数更新步长的超参数。

• loss = criterion(y_pred, y_data) :criterion 是之前定义的损失函数，在这里使用的是均方误差损失（MSELoss）。

• optimizer.zero_grad() : 清除所有优化器管理的参数的梯度。默认情况下，梯度是累加的，因此在每次反向传播前需要清除梯度。

• loss.backward() : 进行反向传播，计算损失相对于模型参数的梯度。

• optimizer.step() : 使用计算出的梯度更新模型参数。

# 常用优化器列表：

1
2
3
4
5
6
7
8
9
10

optimizers = [
    optim.Adagrad,
    optim.Adam,
    optim.Adamax,
    optim.ASGD,
    optim.LBFGS,
    optim.RMSprop,
    optim.Rprop,
    optim.SGD
]

# 激活函数$\sigma$ 介绍

一般情况下$\sigma$ 默认为逻辑斯特函数

# 逻辑斯特函数

$$\sigma(x)=\frac{1}{1+e^{-x}}$$

# 误差函数（Error Function）

$$\mathrm{erf}\left(\sqrt{\frac{\pi}{2}} x \right)$$

• 定义： erf(x) 是在概率、统计以及偏微分方程中广泛使用的特殊函数。
• 用途：主要用于正态分布中的积分计算。

# 双曲正切函数

$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

• 用途：常用作神经网络中的激活函数。其输出范围为 [-1, 1]，有助于将输入值压缩到有限范围内。

# Gudermannian 函数

$$\frac{2}{\pi} \mathrm{gd}\left(\frac{\pi}{2} x \right)$$

• 用途：用于数学中的一些特殊变换，尽管在神经网络中不常见。

# ArcSinh 激活函数的倒数形式

$$\frac{x}{\sqrt{1 + x^2}}$$

• 用途：作为一种平滑的激活函数。

# 归一化的反正切函数

$$\frac{2}{\pi} \arctan\left(\frac{\pi}{2} x \right)$$

• 用途：在神经网络中作为激活函数，输出范围为 [-1, 1]。

# 软符号函数

$$\frac{x}{1 + |x|}$$

• 用途：用于神经网络中的激活函数，将输入值压缩到 [-1, 1] 范围内。

# 逻辑斯特回归

# minist 数据集

1
2
3
4
5

import torchvision

train_set = torchvision.datasets.MNIST(root='./dataset/mnist', train=True, download=True)
test_set = torchvision.datasets.MNIST(root='./dataset/mnist', train=False, download=True)

• train_set 加载的是训练数据集（ train=True ）。
• test_set 加载的是测试数据集（ train=False ）。
• root 参数指定了数据集的存储路径。
• download=True 表示如果数据集不存在，则从互联网下载数据集。
• mnist 数据集：
  

# CIFAR-10 数据集

• 训练集提供了：50000 个样本
• 测试集提供了：10000 个样本
• 分为十个类
• 二分类问题：只有一和零的区别

# 损失函数

$$loss=-(ylog\hat y+(1-y)log(1-\hat y))$$

# 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import torch
import torch.nn.functional as F

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x))
        return y_pred

model = LogisticRegressionModel()

criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

• criterion=torch.nn.BCELoss(size_average=False) ：损失函数 - 交叉熵
• optimizer = torch.optim.SGD(model.parameters(), lr=0.01) : 采用 SGD 优化器