Home HKUST_RA

# 自适应消息传递增强图异常检测

# A B S T R A C T

  • 现有方法主要集中在（局部不一致挖掘）LIM 上 —— 基于很难在异常节点与其邻居之间建立高相似性的直觉
  • 图神经网络 (gnn) 采用的消息传递导致局部异常信号丢失，因为 gnn 倾向于使连接节点相似，这与 LIM 直觉相冲突。
  • 在本文中，提出了 GADAM，这是一个新的框架，它不仅解决了 LIM 和消息传递之间的冲突，而且利用消息传递通过一种超越 LIM 的异常挖掘方法来增强异常检测。
  • 首先提出一种有效的基于 mlp 的 LIM 方法，以无冲突的方式获得局部异常分数。
  • 接下来介绍了一种从全局角度捕获异常信号的新方法。
  • 涉及到基于混合注意的自适应信息传递，使节点能够选择性地从周围环境中吸收异常或正常信号。
  • 在 9 个基准数据集 (包括 2 个大规模 OGB 数据集) 上进行的大量实验表明，GADAM 在有效性和效率方面都优于现有的最先进方法

# LIM：局部不一致性挖掘

局部不一致性挖掘 (LIM) 是一种在图异常检测中常用的方法。LIM 基于这样一个直观假设：异常节点与其邻居之间的特征相似性通常较低。这是因为异常节点往往具有与周围节点明显不同的属性或连接模式。因此，通过测量一个节点与其邻居之间的特征或连接模式的不一致性，可以识别出潜在的异常节点。

  • 特征表示：每个节点都用一个特征向量来表示。这些特征可以从节点的属性（如节点的标签、嵌入向量等）中提取。对于不同的应用场景，特征的类型和维度可能有所不同。
  • 相似性计算：然后，LIM 通过计算特征向量之间的相似性来评估节点之间的特征相似性。常用的相似性度量方法包括余弦相似性、欧氏距离、Jaccard 相似性等。具体选择哪种度量方法取决于特征向量的特性。
  • 局部相似性评估：LIM 关注的是局部相似性，即每个节点与其邻居之间的相似性。因此，它计算每个节点与其邻居节点的特征相似性。通过这种方式，LIM 可以得到局部图中每个节点与其邻居之间的相似性分布。

具体原理：

  • 局部特征相似性计算：首先，LIM 计算每个节点与其邻居之间的特征相似性，如上文所述。
  • 不一致性度量：然后，LIM 对每个节点计算一个不一致性得分。这通常通过统计节点与其邻居之间相似性的分布来实现。若某个节点的特征与大多数邻居的特征显著不同，则其不一致性得分较高。具体计算方法可能包括：
    • 相似性均值差异：计算节点特征向量与其邻居特征向量的平均相似性差异。
    • 基于熵的度量：利用熵来度量相似性分布的集中度，熵越大，不一致性越高。
  • 异常检测：根据不一致性得分，LIM 可以识别图中的异常节点或异常子图。高不一致性得分的节点被认为是与其局部环境不一致的，因此可能是异常的。
  • 结果分析和解释：最后，LIM 的输出结果是一个不一致性得分的排序列表。研究人员或算法可以根据这个列表进一步分析潜在的异常点，或者将这些异常点作为标记数据来进行进一步的学习和优化。

# LIM 工作流程

  • 节点特征提取：首先，需要提取图中每个节点的特征。这些特征可以包括节点的属性（如在社交网络中，用户的个人信息）或结构特征（如节点的度、邻居的平均属性等）。
  • 相似性度量：然后，计算每个节点与其邻居之间的相似性。常见的相似性度量包括欧氏距离、余弦相似性等。
  • 不一致性计算：对于每个节点，通过计算其与邻居之间的相似性，来衡量其与邻居的不一致性。通常，不一致性较高的节点被认为是异常的。
  • 异常分数计算：最后，将不一致性值转换为异常分数。通常，不一致性越高，异常分数也越高。

# LIM 与 GNN 消息传递机制的冲突

  • 图神经网络 (GNN) 是一种通过消息传递机制来学习节点表示的方法。在 GNN 中，节点的表示是通过聚合其邻居节点的特征来更新的。这种消息传递的基本思想是：通过反复将节点的邻居信息传递给节点本身，使得图中的每个节点逐渐拥有其局部邻域的综合信息。

# GNN 消息传递机制

  • 特征聚合：在每一层 GNN 中，每个节点会从其直接邻居中收集信息（即消息传递），这些信息通常以邻居节点的特征表示。
  • 特征更新：节点通过聚合其邻居的特征（例如，通过求和或取平均）来更新自身的特征表示。
  • 多层聚合：GNN 通过多层次的聚合，使得每个节点可以间接地从更远的节点获取信息，最终形成一个综合的节点表示。

# 冲突解释

  1. 特征趋同现象：由于 GNN 的消息传递机制会聚合邻居节点的特征，这意味着与一个节点相邻的节点，其特征会逐渐变得相似。随着消息传递层数的增加，这种相似性会逐渐扩展到更大的邻域。** 这与 LIM 的基本假设 —— 异常节点与其邻居之间的特征相似性较低 —— 直接矛盾。**GNN 的特征聚合会导致异常节点的特征与其邻居的特征更加相似，从而掩盖了这些异常信号。
  2. 异常信号丢失：GNN 的特征聚合倾向于将相邻节点的特征进行平滑处理，从而使得节点之间的差异性降低。这种平滑处理的效果是，原本应当突显出来的异常节点反而被 “冲淡” 了，导致异常信号在聚合过程中丢失。
  3. 局部不一致性的减弱：LIM 依赖于检测节点与邻居之间的局部不一致性，但 GNN 的消息传递会增强节点与其邻居之间的相似性，这直接削弱了局部不一致性挖掘的效果。因此，基于 GNN 的 LIM 可能无法有效区分正常节点与异常节点，因为它们的特征变得更加相似，局部不一致性被弱化。

# I N T R O D U C T I O N

# 图异常节点类型

# 上下文异常

上下文异常指的是那些节点的属性与其邻居节点属性显著不同的情况。换句话说，这些节点的特征在其局部上下文（即邻居节点的集合）中显得不合常理。

** 判断依据：** 在图数据中，上下文异常的节点可能具有与其周围邻居完全不同的属性。例如，在社交网络中，某个用户的兴趣标签与其好友的兴趣标签有显著不同，就可能被视为上下文异常。

  • 可以通过比较每个节点与其邻居的属性差异来判断是否为上下文异常。
  • 具体方法可能包括计算节点属性与其邻居属性的相似性（如欧氏距离、余弦相似度），如果该相似度低于某个阈值，则该节点可能是上下文异常。

# 结构异常

结构异常指的是在图的连接结构上表现异常的节点。具体来说，结构异常节点的连接模式与正常节点不同，可能表现为连接密度异常高或异常低。

连接密度异常：结构异常的节点可能在邻域内有着过多或过少的连接。例如，某些节点可能与非常多的其他节点形成连接（形成团块），这可能是不正常的。

连接模式异常：某些节点可能与通常不会连接的其他节点形成连接，这也是一种结构异常。

方法：

  • 可以通过分析节点的度数（与之相连的边的数量）以及邻域内的连接密度来判断是否为结构异常。
  • 例如，如果某个节点的度数明显高于或低于其所在图的平均度数，这可能是结构异常。

尽管消息传递存在这些潜在的问题，但完全舍弃消息传递并不可取。这是因为图结构中存在的许多有价值的信息（例如，结构异常）仍然需要通过消息传递机制来捕捉和利用。因此，解决方案不应是简单地取消消息传递，而应是设计一种能够在保留消息传递优势的同时，减轻其对异常检测负面影响的方法。

# 现有优化方法及存在的问题

  • 这些方法旨在增强异常的局部显著性并产生可区分的表示，通常利用注意机制来减少异常节点与其相邻节点之间的消息传递，从而增强异常信号的局部显著性并产生更具区分性的节点表示。—— 这这些方法主要适用于发现上下文异常（Contextual Anomalies），即那些特征与周围邻居显著不同的节点。对于这类异常，减少与邻居之间的消息传递有助于保持异常特征的突出性。
  • 结构异常结构异常的挑战结构异常（Structural Anomalies）通常表现为具有相似特征和异常行为的节点集群。由于这些节点倾向于形成共享相似属性和行为的簇，简单地减少或阻止消息传递可能会与这种结构异常的固有性质冲突。这意味着现有方法在处理结构异常时可能效果不佳，因为这些方法试图通过减少消息传递来保持节点之间的特征差异，而结构异常的性质要求维护这种异常节点的集群一致性
  • 现有半监督方法的尝试：一些半监督方法通过精细化的消息传递和合理的异常挖掘策略在一定程度上提高了性能。然而，即使是这些改进的半监督方法，也仍然没有完全解决这个问题。

# Our Work——UGAD

  • 通过对消息传递的精心控制来确保无冲突的 LIM
  • 在没有标签的情况下，实现对节点特定消息与其邻居之间传递的细粒度控制
  • 设计新的学习目标和超越 LIM 的异常挖掘方法，利用消息传递的效用增强异常检测。

Graph Anomaly Detection with Adaptive Message passing（基于自适应消息传递的图异常检测）：

  • 我们提出了 GADAM1 (图异常检测与自适应消息传递)，一个清晰灵活的两阶段框架，执行 LIM 和消息传递解耦。在第一阶段，我们提出了一种基于 mlp 的无消息传递的 LIM 对比方法，使 LIM 能够更有效地从局部角度识别异常节点并产生异常分数。在第二阶段，我们将学习目标转换为二元分类任务，利用局部异常分数作为伪标签。具体而言，利用第一阶段的局部异常分数建立两个高置信度的正常和异常节点集。
  • 随后，我们定义了学习目标，以区分节点与全局正常上下文 (即高置信度正态节点的平均值) 之间的对齐，并从全局视图生成异常分数。第二阶段将进行半监督训练，由伪标签引导，并由自适应消息传递方案促进。为了实现具有不同角色节点的自适应消息传递，我们进一步提出了一种创新的混合注意机制，该机制既考虑异常评分差异，又考虑与相邻节点的特征相似性。
  • 异常挖掘视角的转变，结合混合注意机制的设计，使消息传递能够丰富异常挖掘，类似于 gnn 中的特征聚合如何增强分类任务 (Huang et al, 2020;Wang & Zhang, 2022; 朱，2005)。两个阶段的异常分数将结合起来，提供节点异常的整体度量。

拆分解析：

  • 第一阶段：基于 MLP 的对比学习（MLP-based Contrastive Learning）
    • 无消息传递的 LIM：在第一阶段，GADAM 采用基于多层感知机（MLP）的对比学习方法，不进行消息传递。这样做的目的是避免 GNNs 中的消息传递机制对 LIM 产生的冲突，确保能够更有效地识别异常节点。
    • 生成局部异常分数：通过对比学习，模型能够从局部视角识别出异常节点，并为每个节点生成一个局部异常分数。
  • 第二阶段：基于伪标签的二分类任务
    • 转换学习目标：在第二阶段，GADAM 将学习目标转换为一个二分类任务。这一阶段利用第一阶段生成的局部异常分数作为伪标签，创建出高置信度的正常节点集和异常节点集。
    • 全局异常检测：在这一阶段，模型通过比较节点与全局正常上下文的对齐情况（全局正常上下文是指高置信度正常节点集的平均值），来生成全局异常分数。这个阶段的训练是半监督的，由伪标签引导，并结合自适应消息传递方案来进行。
  • 自适应消息传递与混合注意力机制
    • 创新的混合注意力机制：为了实现对具有不同角色节点的自适应消息传递，GADAM 提出了一种创新的混合注意力机制。这个机制结合了节点与其邻居之间的异常分数差异以及特征相似性，来精细地调整消息传递的强度。
    • 异常挖掘视角的转变：通过这种混合注意力机制，消息传递在异常挖掘中得到了有效的应用，类似于 GNNs 在分类任务中通过特征聚合来提升效果。
  • 综合异常分数
    • 多维度的异常检测：GADAM 通过结合来自第一阶段的局部异常分数和第二阶段的全局异常分数，为每个节点生成一个综合的异常分数。这个分数能够全面衡量节点的异常程度。

GADAM 提出了一种新颖的、基于两阶段方法的图异常检测框架，通过解耦 LIM 和消息传递，使得在不丢失图结构信息的前提下，更加有效地检测异常节点。创新的混合注意力机制进一步增强了消息传递的适应性，使得模型能够更好地应对不同类型的异常信号。

# 具体贡献

分析现有 UGAD 方法在处理消息传递时遇到的困境：

  • GADAM 方法首先分析了当前无监督图异常检测（UGAD）方法在处理消息传递时面临的困境。传统的 LIM 方法在与 GNNs 结合时容易发生冲突，为了解决这一问题，GADAM 引入了一种基于 MLP 的对比学习方法，旨在将消息传递与 LIM 解耦，从而提高 LIM 的效果和效率。

提出了一种从全局视角进行异常挖掘的新方法：

  • GADAM 不仅在局部进行异常挖掘，还引入了从全局视角进行异常挖掘的新方法。这种方法利用局部异常分数作为伪标签，将异常检测任务转换为一个二分类任务，从而促进消息传递的有效性，并增强异常检测的效果。

设计了一个精细的混合注意力机制：

  • 为了实现更精确和自适应的消息传递，GADAM 提出了一个设计精良的混合注意力机制。该机制综合考虑了节点的异常分数差异和与邻居的特征相似性，使得消息传递能够更加自适应地调整，从而更准确地进行异常检测。

广泛的实验结果：

  • 在九个基准数据集上的广泛实验结果表明，GADAM 方法在效果和效率上均优于现有的方法。这些数据集包括七个注入了合成异常的数据集和两个包含自然异常的数据集。实验结果证明，GADAM 在与多种基线方法的比较中达到了最先进的性能水平。此外，GADAM 在运行时间和 GPU 资源消耗方面也表现出了明显的优势。

# B A C K G R O U N D

# 无监督图异常检测

image.png

# UGAD 的对比学习

image.png

CoLA 是第一个将对比学习用于 LIM 的研究，其过程可分为四个部分。

image.png

# N O T E S

  • 在 2 末尾添加，EpiE^i_p 表示Gpi\mathcal G_p^i 中的节点嵌入。接下来，利用参数WW 和激活函数ϕ\phi 与GCNGCN 相同的II 层前馈网络 (FFN) 将节点viv_i 映射到相同的特征空间hi=FFN(X[i,:];W,ϕ)h_i=FFN(X[i,:];W,\phi)

  • 在推理阶段，对节点viv_i 采样RR 个正子图和负子图，形成实例池(Gpi,1,...,Gpi,R,...,Gni,1,...,Gni,R)(\mathcal G_p^{i,1},...,\mathcal G_p^{i,R},...,\mathcal G_n^{i,1},...,\mathcal G_n^{i,R})。然后通过RR-round 评估函数得到异常评分。

    • ** 上标 $ i∗∗：表示与节点**：表示与节点 v_i 相关的子图（实例）。即，所有这些子图相关的子图（实例）。即，所有这些子图 G^i_p$ 和 GniG^i_n 都是从以节点 $ v_i$ 为中心的图中采样的，目的是生成与节点 viv_ivi 相关的正例和负例。

      上标 $ R$：表示多次采样。具体来说，这意味着从图中多次采样（共 RR 次），以生成不同的正子图和负子图。在实例池中，Gpi,1G^{i,1}_p 到 $ G^i,R}_p$ 是第 $i $ 个节点的 $R $ 个正子图，$G({i,1)_n到到 G^{i,R}_n$ 是第 $ i 个节点的个节点的 R $ 个负子图。

      ** 下标 pp 和nn **：

      • pp 代表 "positive"（正例），即与节点 $ v_i$ 相关联的正子图。
      • nn 代表 "negative"（负例），即与节点 viv_i 无关或反映负面的子图。

# THE PROPOSED METHOD

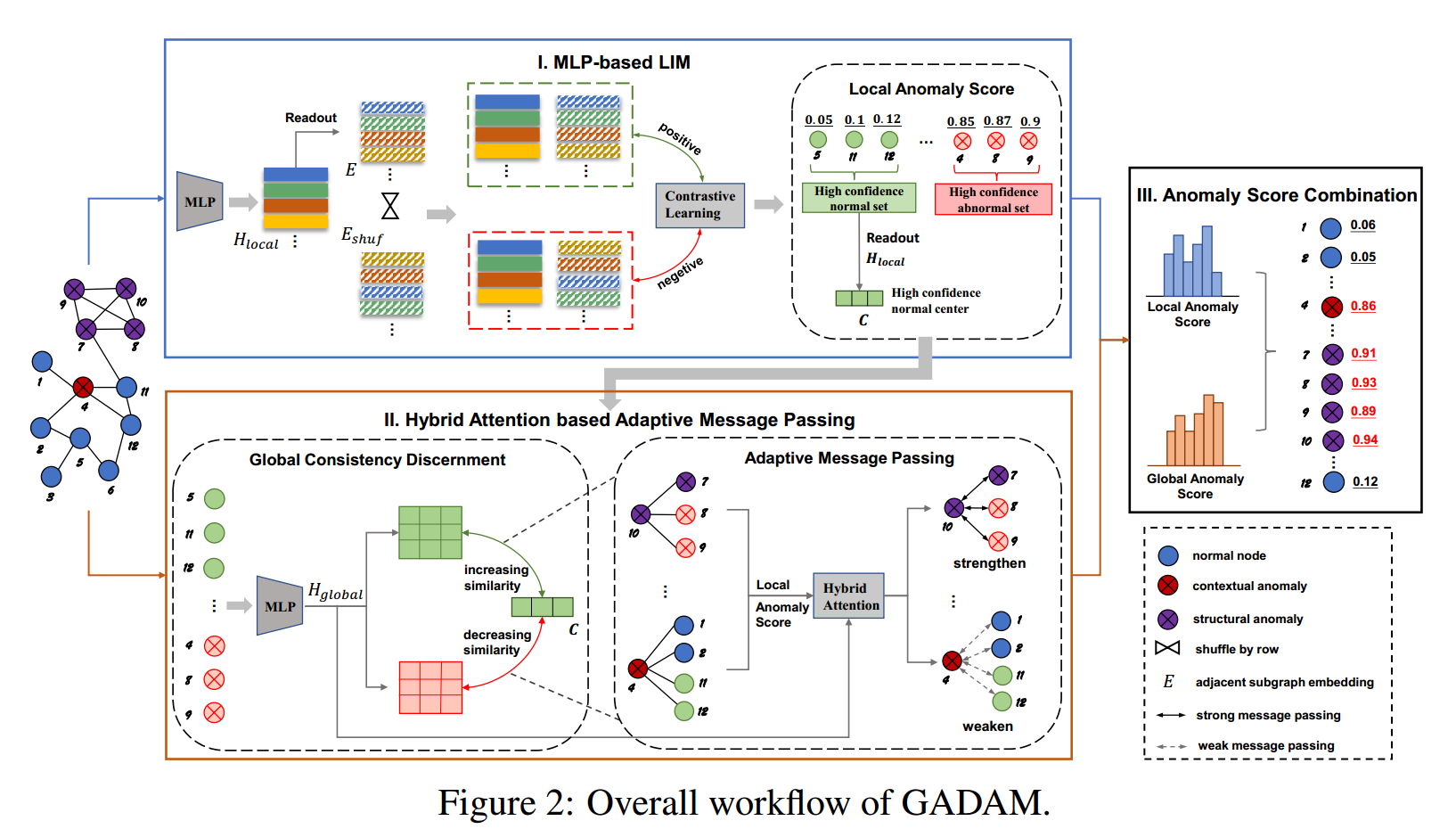
image.png

# 分析

GADAM 采用一个两阶段的框架来进行图异常检测，结合了 MLP（多层感知机）和混合注意力机制进行自适应消息传递，最终生成局部和全局的异常分数。以下是对该流程图的详细解释：

# I. 基于 MLP 的 LIM 阶段（MLP-based LIM）

  1. 输入与初步处理：
    • 首先，从输入图（左侧）中提取每个节点的特征表示，并将其输入到一个多层感知机（MLP）中，以生成初步的节点嵌入表示 $ H_{\text {local}}$
  2. 节点表示和子图表示：
    • 使用 Readout 操作对每个节点生成的嵌入 $ H_{\text {local}}进行处理，生成节点和子图的表示进行处理，生成节点和子图的表示 E$。
    • 同时，为了构建对比学习的实例对，将子图嵌入表示 $E 进行行打乱（Shufflebyrow），以生成负例子图嵌入表示进行行打乱（Shuffle by row），以生成负例子图嵌入表示 E_{\text {shuf}}$。
  3. 对比学习（Contrastive Learning）：
    • 通过对比学习框架，将节点嵌入表示与正例子图嵌入（EE）配对，形成正例对；将节点嵌入表示与负例子图嵌入（EshufE_{\text{shuf}}）配对，形成负例对。通过训练模型识别这些对的相似性或差异性，来识别异常节点。
    • 这个过程的目标是确保异常节点与其邻居的子图表示保持较大的不一致性，从而提高异常检测的效果。
  4. 局部异常分数生成：
    • 基于对比学习生成的异常节点和正常节点的嵌入表示，计算每个节点的局部异常分数。局部异常分数越高，表示节点的异常程度越高。
    • 然后，将节点根据局部异常分数划分为高置信度的正常节点集合（绿色标记）和高置信度的异常节点集合（红色标记）。

# II. 基于混合注意力的自适应消息传递阶段（Hybrid Attention-based Adaptive Message Passing）

  1. 全局一致性辨别（Global Consistency Discernment）：
    • 使用从第一阶段获得的高置信度正常节点集合 $C $ 作为参考，通过与其他节点的表示进行比较，计算出全局一致性分数。这个过程通过评估节点的全局相似性来识别异常。
    • 节点的全局一致性分数用于指导接下来的消息传递过程，以决定哪些节点需要更多的信息传递，哪些节点需要减少信息传递。
  2. 自适应消息传递（Adaptive Message Passing）：
    • 使用混合注意力机制，对消息传递的强度进行自适应调整。
    • 根据局部异常分数和全局一致性分数，增强那些异常程度高或与其邻居差异较大的节点的消息传递强度（实线箭头表示强消息传递），并减弱那些异常程度低或与其邻居相似的节点的消息传递强度（虚线箭头表示弱消息传递）。
    • 这样，模型能够更好地捕捉图结构中的异常信号，尤其是对于那些可能被传统 GNN 平滑掉的异常节点。

# III. 异常分数组合（Anomaly Score Combination）

  1. 局部与全局分数的结合：
    • 最终，来自第一阶段的局部异常分数与第二阶段的全局异常分数相结合，形成每个节点的综合异常分数。
    • 局部异常分数捕捉了节点与其局部邻域的不一致性，而全局异常分数则反映了节点在全局图结构中的异常程度。
  2. 最终输出：
    • 综合异常分数可以用于最终的异常节点检测。分数越高的节点（如图中标记的节点 7、9、10）表示其异常程度越高，可能是图中的异常节点。

# 详解

# 基于 mlp 的本地不一致挖掘

# MLP 作为编码器

  • 通过使用多层感知机（MLP）而非图神经网络（GNN）来生成节点的嵌入表示，避免了消息传递过程中可能产生的冲突。

Hlocal(l)=σ(Hlocal(l−1)W(l−1)+b(l−1))Hlocal(l)[i,:]=Hlocal(l)[i,:]∣∣Hlocal(l)[i,:]∣∣2Hlocal(0)=X\mathbf{H}_{local}^{(l)}=\sigma(\mathbf{H}_{local}^{(l-1)}\mathbf{W}^{(l-1)}+\mathbf{b}^{(l-1)})\\ \mathbf{H}_{local}^{(l)}[i,:]=\frac{\mathbf{H}_{local}^{(l)}[i,:]}{||\mathbf{H}_{local}^{(l)}[i,:]||_{2}}\\ \mathbf{H}_{local}^{(0)}=\mathbf{X}

  • L2 范数计算公式:||\mathbf{v}||_2=\sqrt
  • MLP 前向传播
  • 然后使用 L2 正则化
    • H(l)local[i:]H^{(l)_{local}[i:]} 表示第ll 层中第ii 个节点的嵌入向量
    • ∣∣H(l)local[i:]∣∣2||H^{(l)_{local}[i:]}||_2 是第ii 个节点的嵌入向量的 L2 范数，也称欧几里得范数
    • 将第ii 个节点的嵌入向量进行归一化，使得 L2 范数等于 1
  • 将初始输入设置为节点的原始特征矩阵XX

# 免样对比对构造

  • 将正实例Gpi\mathcal G_p^i 作为节点viv_i 的完全邻接子图而不是用采样。

  • 对GpiG_p^i 中的节点嵌入进行平均计算，得到子图的嵌入表示epie_p^i

  • 计算方法：正例子图的嵌入表示 epie^i_p 是通过对该子图中所有节点的嵌入表示取平均得到的。这里，嵌入表示矩阵E\mathbf{E} 是通过 MLP 生成的，每行E[i,:]\mathbf{E}[i,:] 对应节点 viv_i 的嵌入 epie^i_p。

  • 负例子图不是通过从其他地方采样生成，而是通过对正例子图的嵌入矩阵E\mathbf{E} 进行行打乱（Shuffle by row）来生成的。这个过程称为 “打乱” 是因为它不改变矩阵的值，但重新排列了各行的顺序，从而破坏了原本嵌入表示的上下文结构。这个打乱的嵌入表示矩阵 EshufE_{\text{shuf}} 被用作负例子图的嵌入表示。

  • 正负例对的表示（Positive and Negative Instance Pairs）:

    pos=⟨hilocal,E[i,:]⟩,neg=⟨hilocal,Eshuf[i,:]⟩\mathrm{pos}=\langle h_i^\mathrm{local},\mathbf{E}[i,:]\rangle,\quad\mathrm{neg}=\langle h_i^\mathrm{local},E_\mathrm{shuf}[i,:]\rangle

    • h_i^{local}$：这是节点 viv_i 的嵌入表示。

      E[i,:]\mathbf {E}[i,:]：这是节点viv_i 对应的正例子图的嵌入表示。

      Eshuf[i,:]E_{\text{shuf}}[i,:]：这是通过打乱生成的负例子图的嵌入表示。

  • 通过采用无采样的方法（即直接使用完整的邻接子图并进行打乱生成负例），避免了传统采样方法的计算开销。这种方法在处理大规模图时尤其有效，因为它减少了图采样所需的时间和计算资源。

# 无参数相似性判别器（Parameter-free Similarity Discriminator）

  • 使用无参数的相似性判别器来比较节点与子图之间的相似性，从而判断它们的相关性。
  • 使用内积（即余弦相似性）作为相似性度量标准。公式定义了节点嵌入与正例子图嵌入以及负例子图嵌入之间的相似性计算方法。
  • 这个判别器不需要额外的参数，通过内积计算节点与子图之间的相似性，进而用于对比学习中的相似性判别。
  • 在 L2 正则化之后，内积与余弦相似性是等价的。因为余弦相似性是通过两个向量的内积除以它们的 L2 范数得到的，而在 L2 正则化后，向量的 L2 范数被归一化为 1，因此内积直接反映了余弦相似性。
  • L2 正则化的作用：通过 L2 正则化，每个嵌入向量的长度被标准化为 1，这意味着内积不仅仅是一个简单的数值计算，而是反映了向量的相对方向一致性。这样可以确保相似性计算的稳定性和合理性。

Dis(hilocal,epi)=hilocal(epi)T,Dis(hilocal,eni)=hilocal(eni)TDis(\boldsymbol{h}_i^{local},\boldsymbol{e}_p^i)=\boldsymbol{h}_i^{local}(\boldsymbol{e}_p^i)^T, Dis(\boldsymbol{h}_i^{local},\boldsymbol{e}_n^i)=\boldsymbol{h}_i^{local}(\boldsymbol{e}_n^i)^T

image.png

# 直接计算节点的局部异常分数（Local Anomaly Score）

  • 异常分数的计算公式如下：

    silocal=−Dis(hilocal,epi)=−hilocal(epi)Ts_i^{local}=-Dis(\boldsymbol{h}_i^{local},\boldsymbol{e}_p^i)=-\boldsymbol{h}_i^{local}(\boldsymbol{e}_p^i)^T

    image.png

# 优化

  • image.png
  • image.png

# 基于混合注意的自适应消息传递

# 混合注意力的自适应消息传递 (Adaptive Message Passing)

image.png

# 混合注意力机制（Hybrid Attention Mechanism）

  • 混合注意力机制的目的是根据节点的特性，为每个节点分配适当的消息传递权重。正常节点和结构异常节点往往与其邻域有更高的一致性，因此需要更高的消息传递权重，而上下文异常节点则通常与其邻域有较大差异，因此消息传递权重应较低。

    # 预注意力（Pre-attention）：

    • 基于节点的局部异常分数与其邻域的差异来计算，如公式所示。对于给定节点viv_i，局部异常分数的差异 δi\delta_i 定义为:

      δi=∣silocal−1∣N(i)∣∑j∈N(i)sjlocal∣\delta_i=|s_i^\text{local}-\frac{1}{|\mathcal{N}(i)|}\sum_{j\in\mathcal{N}(i)}s_j^\text{local}|

    • N(i)\mathcal N(i) 是节点viv_i 的邻域节点的集合

    • sjlocals_j^{local} 是邻域节点jj 的局部异常分数

  • 标准差计算：

    • 计算差异δi\delta_i 的标准化偏差did_i 的公式如下:

      di=∣δi−Ej∈Vn(δj)∣Varj∈Vn(δj)d_i=\frac{|\delta_i-\mathbb{E}_{j\in V_n}(\delta_j)|}{\mathrm{Var}_{j\in V_n}(\delta_j)}

      • 这里，Ej∈Vn(δj)\mathbb{E}_{j\in V_n}(\delta_j) 是高置信度正常节点集VnV_n 中节点的平均差异，Varj∈Vn(δ)jVar_{j\in V_n}(\delta)j 是这些节点差异的方差

  • 预注意力的计算：

    • 通过激活函数 σ(di)\sigma(d_i) 将标准化偏差did_i 转换为预注意力得分 $ \text {pre}_i$，如公式所示：

      prei=1−σ(di)\mathrm{pre}_i=1-\sigma(d_i)

      直观上，正常节点和结构异常节点的δi\delta_i 较小，预注意力得分较高，而上下文异常节点的 δi\delta_i 较大，预注意力得分较低。
# 后注意力（Post-attention）
  • 相似性计算：

    posti=higlobal(epi)T\mathrm{post}_i=h_i^\mathrm{global}(e_p^i)^T

    这个相似性反映了节点与其邻域在全局上下文中的一致性
# 动态加权求和（Dynamic Weighted Sum）
  • ** 权重计算：** 将预注意力和后注意力动态加权求和，得到最终的自适应权重系数：

    αi(t)=β(t)⋅prei+(1−β(t))⋅posti其中,β(t)是一个动态权重系数,随着训练轮次t的增加而变化:β(t)=β×(1−tTglobal)∙这里,Tglobal 是第二阶段的总训练轮次,β是初始的预注意力权重,通常小于1。\begin{gathered} \alpha_{i}^{(t)}=\beta(t)\cdot\mathrm{pre}_{i}+(1-\beta(t))\cdot\mathrm{post}_{i} \\ \text{其中,}\beta(t)\text{ 是一个动态权重系数,随着训练轮次 }t\text{ 的增加而变化}: \\ \beta(t)=\beta\times\left(1-\frac{t}{T_{\mathrm{global}}}\right) \\ \bullet\quad\text{这里,}T_\text{global 是第二阶段的总训练轮次,}\beta\text{ 是初始的预注意力权重,} \\ \text{通常小于1。} \end{gathered}

# 全局一致性识别

异常节点往往与全局正常上下文（CC）的距离更远，而正常节点则更接近于全局正常上下文。因此，通过增强高置信度正常节点集（VnV_n）与全局正常上下文的相似性，同时减少高置信度异常节点集（VaV_a）与全局正常上下文的相似性，可以有效地区分异常节点和正常节点。

本部分的目标是通过全局一致性辨别，进一步提升模型识别异常节点的能力。具体来说，就是要通过构造合适的损失函数来优化节点与全局正常上下文之间的相似性，进而计算出全局异常分数。

损失函数构造：

相似性度量（gig_i）：

节点vi与全局正常上下文C的相似性度量为:gi=Dis(himix,C)=himixCT∙这里,himin⁡是节点vi的混合嵌入表示,而C是全局正常上下文(由高置信度正常节点集Vn的嵌入表示的均值构成)。\begin{gathered} \text{节点 }v_i\text{ 与全局正常上下文 }C\text{ 的相似性度量为:} \\ g_{i}=\mathrm{Dis}(h_{i}^{\mathrm{mix}},C)=h_{i}^{\mathrm{mix}}C^{T} \\ \bullet\quad\text{这里,}h_i^{\min}\text{ 是节点 }v_i\text{ 的混合嵌入表示,而 }C\text{ 是全局正常上下文} \\ (\text{由高置信度正常节点集 }V_n\text{ 的嵌入表示的均值构成)。} \end{gathered}

损失函数（L)：

  • 构造的损失函数旨在最大化高置信度正常节点集中的节点与全局正常上下文的相似性，同时最小化高置信度异常节点集与全局正常上下文 的相似性

L=−1∣Vn∣+∣Va∣(∑j∈Vnlog⁡(gj)+∑k∈Valog⁡(1−gk))L=-\frac{1}{|V_n|+|V_a|}\left(\sum_{j\in V_n}\log(g_j)+\sum_{k\in V_a}\log(1-g_k)\right)

image.png

全局异常分数：

对每个节点viv_i，全局异常分数由其与全局正常上下文CC 的相似性度量gig_i 得到：

Siglobal=−giS_i^{global}=-g_i

这里通过取相反数，使得与CC 的相似性越低（即 gig_i 越小）的节点，全局异常分数越高，从而更可能被认为是异常节点

最终异常分数（S)：

最后,将局部异常分数Slocal和全局异常分数Sglobal结合,生成最终的异常分数:S=(Slocal+Sglobal)2∙通过结合局部和全局信息,最终的异常分数能够更准确地反映节点的异常程度。\begin{aligned} &&&\text{最后,将局部异常分数 }S^{\mathrm{local}}\text{ 和全局异常分数 }S^{\mathrm{global}}\text{ 结合,生成最终的} \\ &&&\text{异常分数:} \\ &&&S=\frac{(S^{\mathrm{local}}+S^{\mathrm{global}})}{2} \\ &&&\bullet \text{通过结合局部和全局信息,最终的异常分数能够更准确地反映节点的} \\ &\text{异常程度。} \end{aligned}

# 效率分析（Efficiency Analysis）

image.png