Home HKUST_RA

# 综述

# 1. 研究背景

  • 移动社交网络的快速发展促进了人们的社会交往，但也导致了网络欺诈行为的增加。这些欺诈行为给个人和社会带来了巨大的经济损失。
  • 检测欺诈用户的常用数据是通话记录（CDR），但这些数据存在严重的不平衡性，这会影响基于 GNN 的欺诈检测模型的效果。

# 2. 问题定义

  • 图不平衡问题：图中正样本和负样本数量不平衡，特别是在社交网络欺诈检测中，欺诈用户仅占所有用户的一小部分。这种不平衡会影响模型的判断和效果。
  • 挑战：主要有两个挑战 ——1) 正节点周围负邻居过多，影响 GNN 的聚合效果；2) 正节点在所有节点中的比例过低，模型难以学习到有效的模式。

# 3. 方法介绍

  • CS-GNN 模型

    ：结合成本敏感学习和 GNN，通过以下两部分解决图不平衡问题：

    • 基于强化学习的邻居采样：通过强化学习动态调整邻居的采样概率，平衡节点周围的正负邻居比例。
    • 成本敏感学习：设计了自动化的成本矩阵学习方法，通过反向传播优化该矩阵，以在不平衡的图上更好地分类节点。

# 4. 实验和结果

  • 实验数据集：使用了两个不平衡的电信欺诈检测数据集（四川数据集和 BUPT 数据集）。
  • 实验结果：CS-GNN 在这两个数据集上的表现优于其他基准方法，特别是在处理图不平衡问题上展现出了显著优势。

# 5. 模型性能分析

  • 不平衡率影响：随着数据集中不平衡率的变化，CS-GNN 依然保持了较好的表现，证明了该方法在处理不平衡图时的鲁棒性。
  • 消融实验：通过去除邻居采样和成本敏感学习模块，验证了这两个模块对最终模型效果的重要性。

# 6. 总结

  • 该研究提出了一种有效解决图不平衡问题的 CS-GNN 模型，通过强化学习和成本敏感学习的结合，显著提高了在移动社交网络欺诈检测中的表现。

# 预备工作

# 符号表

image.png

# 图失衡定义

在一组图节点中，设有 K 个类别 C1,C2,…,CK{C_1, C_2, \dots, C_K}. 其中 ∣Ci∣|C_i| 表示第 i 类的样本数量。图不平衡问题是指这些类别中的样本数量存在显著差异。

为了量化图的不平衡程度，文中引入了一个不平衡率IRIR，其定义如下：

IR=min⁡i(∣Ci∣)max⁡i(∣Ci∣)IR = \frac{\min_i(|C_i|)}{\max_i(|C_i|)}

取值范围: IRIR 的取值范围为 [0, 1]。如果 IR<1IR < 1，意味着图是不平衡的（即某些类别的样本数明显少于其他类别）。当IR=1IR = 1 时，图是平衡的（即所有类别的样本数相等）。

# 成本敏感学习（Cost Sensitive Learning）

  • 成本敏感学习 是一种训练分类器的方法，通过为不同类别样本的错误分类赋予不同的惩罚来进行学习。与传统的尽可能减少错误分类率的方法不同，成本敏感学习侧重于在分类决策中引入不同类型的错误分类成本，以减少总体的错误分类成本。

# 成本矩阵CC

成本敏感学习的核心在于定义一个错误分类成本矩阵 $ C$。这个矩阵的每个元素 CijC_{ij} 表示将类别 $i $ 的样本错误分类为类别 jj 的惩罚成本。通常情况下，类别数为KK，则成本矩阵 $C 的维度为的维度为 K \times K$。

矩阵形式：

C=[C10C11⋯C1KC20C21⋯C2K⋮⋮⋱⋮CK0CK1⋯CKK]C=\begin{bmatrix}C_{10}&C_{11}&\cdots&C_{1K}\\C_{20}&C_{21}&\cdots&C_{2K}\\\vdots&\vdots&\ddots&\vdots\\C_{K0}&C_{K1}&\cdots&C_{KK}\end{bmatrix}

CijC_{ij} 的值越大，表示该错误分类的损失越大

# 基于 GNN 的社交网络欺诈

构建一个社交行为图G=(V,X,A,E,Y)。其中:∙V={v1,v2,v3,...vN}表示节点集合,即订阅者的集合。∙X=x1,X2,...,xN是订阅者原始行为的特征集合。其中xi∈R是订阅者vi的行为特征向量。这些特征向量组成一个矩阵，即图G的特征矩阵X∙A∈RN×N是图G的邻接矩阵,其中ai,j=1表示节点i和节点j之间存在边,如果没有边则ai,j=0。∙E代表的是图中的边集合∙Y={y1,y2,...,yn}是标签的集合。\begin{aligned} &构建一个社交行为图G=(\mathcal{V},\mathcal{X},\mathcal{A},\mathcal{E},\mathcal{Y})。 \\ &\text{其中:} \\ &\bullet\quad\mathcal{V}=\{v_1,v_2,v_3,...v_N\}\text{ 表示节点集合,即订阅者的集合。} \\ &\bullet\quad\mathcal X={x_1,X_2,...,x_N}是订阅者原始行为的特征集合。其中x_i\in\mathbb R\\&是订阅者v_i的行为特征向量。这些特征向量组成一个矩阵，即图G的特征矩阵X \\ &\bullet\quad\mathcal{A}\in\mathbb{R}^{N\times N}\text{ 是图 }G\text{ 的邻接矩阵,其中 }a_{i,j}=1\text{ 表示节点 }i\text{ 和节点 }j\text{ 之} \\ &\text{间存在边,如果没有边则 }a_{i,j}=0。 \\ &\bullet \quad\mathcal E 代表的是图中的边集合 \\ &\bullet\quad\mathcal{Y}=\{y_1,y_2,...,y_n\}\text{ 是标签的集合。} \end{aligned}

# GNN 的中间层传递公式

对于给定的移动社交网络，GNN 可以用于节点嵌入学习。GNN 中层间的传递公式可以形式化地表示为：

hv(l)=σ(hv(l−1)⊕Agg{hv′(l−1):(v,v′)∈E})′:′约束条件，表示只有满足后面条件的节点才会被考虑其中:∙hv(l)表示第l层中节点v的嵌入,hv(0)=xv是节点v的初始特征。∙v′是节点v的邻居节点。Agg()是用于邻居特征聚合的消息聚合函数,比如平均聚合(meanaggregation)、池化聚合(pooling aggregation)、注意力聚合(attention aggregation)等。σ是激活函数。⊕表示特征的连接或求和操作。\begin{aligned} & h_{v}^{(l)}=\sigma\left(h_{v}^{(l-1)}\oplus\mathrm{Agg}\left\{h_{v^{\prime}}^{(l-1)}:(v,v^{\prime})\in\mathcal{E}\right\}\right) \\ &':'约束条件，表示只有满足后面条件的节点才会被考虑\\ &\text{其中:} \\ &\bullet\quad h_v^{(l)}\text{ 表示第 }l\text{ 层中节点 }v\text{ 的嵌入,}h_v^{(0)}=x_v\text{ 是节点 }v\text{ 的初始特征。} \\ &\begin{array}{cc}\bullet \quad&v^{\prime}\text{ 是节点 }v\text{ 的邻居节点。}\end{array} \\ &Agg()是用于邻居特征聚合的消息聚合函数,比如平均聚合(mean \\ &\text{aggregation)、池化聚合(pooling aggregation)、注意力聚合} \\ &\text{(attention aggregation)等。} \\ &\sigma\text{ 是激活函数。} \\ &\oplus\text{ 表示特征的连接或求和操作。} \end{aligned}

# 模型建立

image.png

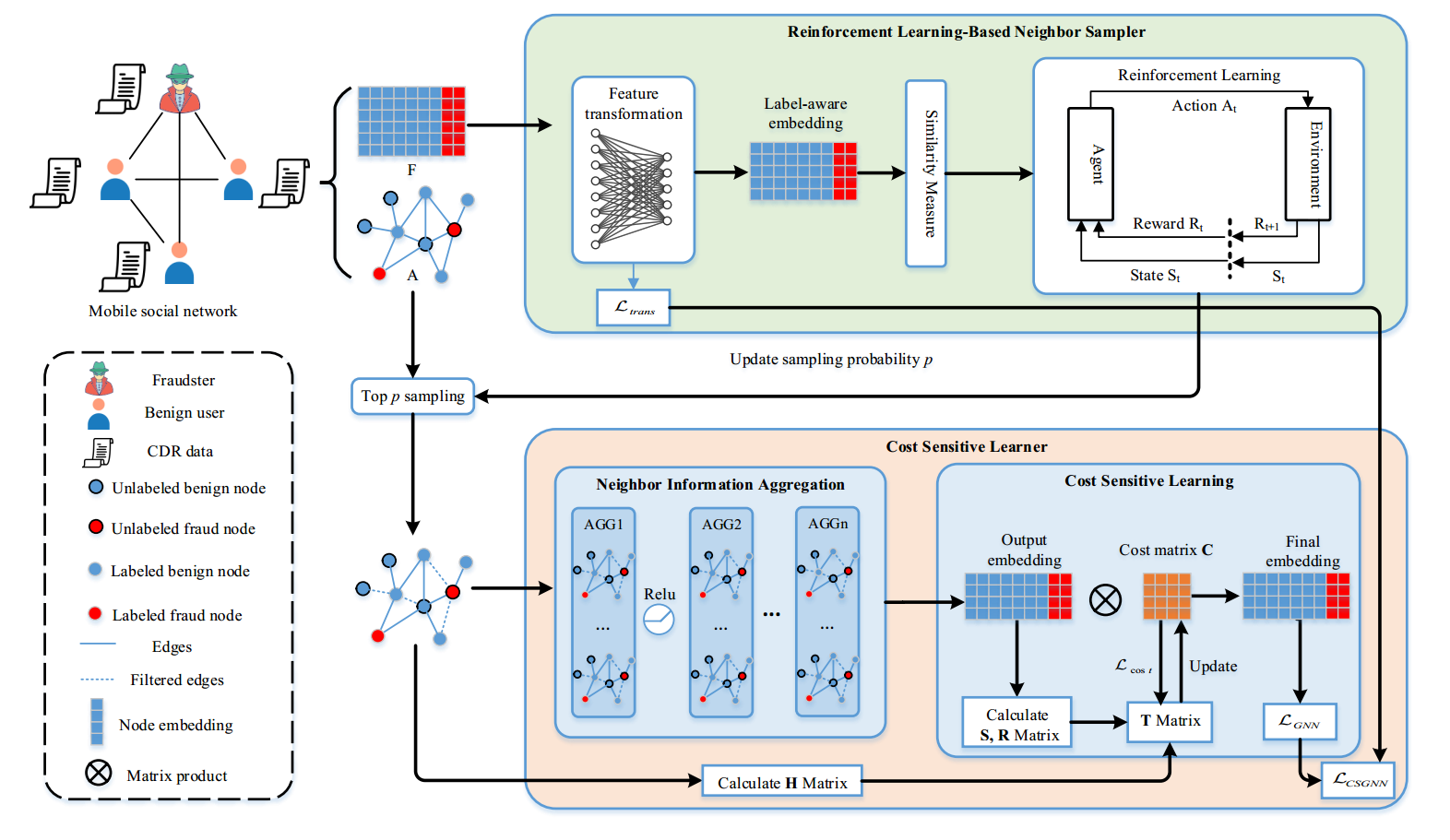
# 整体概述

# 1. 整体流程概述（Pipeline Overview）

  • 图的输入：首先，将一个图输入到基于强化学习的邻居采样器中。这个图代表了移动社交网络，其中节点代表用户，边代表用户之间的联系。

# 2. 基于强化学习的邻居采样器（Reinforcement Learning-Based Neighbor Sampler）

  • 特征转换（Feature transformation）：通过特征转换将原始输入特征转换为适合 GNN 处理的特征向量。
  • 标签感知嵌入（Label-aware embedding）：根据标签信息生成嵌入表示。
  • 相似度度量（Similarity Measure）：计算节点之间的相似度。
  • 强化学习模块（Reinforcement Learning Module）：使用强化学习方法动态调整邻居的采样概率 $ p$，根据相似度排序后，进行 top-p 采样，选择最相似的邻居节点。

# 3. 成本敏感学习器（Cost Sensitive Learner）

  • 邻居信息聚合（Neighbor Information Aggregation）：在 GNN 中使用信息聚合函数（如平均聚合、池化聚合等）对节点的邻居信息进行聚合，以获得节点的嵌入表示。
  • 成本敏感学习（Cost Sensitive Learning）: 通过成本敏感矩阵 $ C$ 对节点嵌入进行转换，以考虑不同类别之间的分类成本。
    • 输出嵌入（Output embedding）：通过成本敏感学习得到节点的最终嵌入表示。
    • 更新矩阵（T Matrix）：根据优化目标 LcostL_{cost} 更新成本敏感矩阵。
    • 最终嵌入（Final embedding）：最终输出的节点嵌入用于分类。

# 4. 最终分类

  • 在得到成本敏感的节点嵌入表示后，模型使用这些嵌入表示进行最终的分类。

# 节点特征转换

  • 根据中心节点和相邻节点的相似性对相邻节点进行采样

  • 使用全连接网络(FCN)(FCN) 作为节点特征转换器，将原始节点vv 的特征xvx_v 转换为嵌入表示hvh_v

  • 转换公式为:

    hv=σ(Wxv)h_v=\sigma(Wx_v)

    其中，σ\sigma 是 ReLU 函数，WW 是需要学习的网络权重矩阵

  • 欧式距离计算节点vv 和邻居节点v′v' 直接的距离，公式为:

    D(v,v′)=∣∣hv−hv′∣∣2∥hv−hv′∥2=∑i(hv,i−hv′,i)2其中hv和hv′分别是节点v和v′的特征向量,hv,i和hv′,i是这些向量的第i个分量。\begin{aligned}& D(v,v')=||h_v-h_{v'}||_2\\ &\|h_v-h_{v^{\prime}}\|_2=\sqrt{\sum_i(h_{v,i}-h_{v^{\prime},i})^2}\\&\text{其中 }h_v\text{ 和 }h_{v^{\prime}}\text{ 分别是节点 }v\text{ 和 }v^{\prime}\text{ 的特征向量,}h_{v,i}\text{ 和 }h_{v^{\prime},i}\text{ 是这些向量的第 }i\text{ 个}\\&\text{分量。}\end{aligned}

  • ** 相似度计算：** 根据计算得到的距离D(v,v′)D(v,v')，可以得到节点vv 与其邻居节点v′v' 的相似度S(v,,v′)S(v,,v'), 公式为：

    S(v,v′)=1−D(v,v′)S(v,v')=1-D(v,v')

  • ** 目标优化：** 使用交叉熵损失函数作为全连接层的优化目标：

    Ltrans=−∑v∈Vyvlog⁡(hv)\mathcal{L}_\text{trans}=-\sum_{v\in\mathcal{V}}y_v\log(h_v)

    yvy_v 是节点vv 的标签，log(hv)log(h_v) 是节点嵌入的对数

# 节点邻居采样

# 状态

  • 每个 epoch 中训练集节点的平均相似度：

    G(S)(e)=∑v,v′∈TrainS(v,v′)∣E(e)∣G(S)^{(e)}=\frac{\sum_{v,v'\in\text{Train}}S(v,v')}{|\mathcal{E}^{(e)}|}

    E(e)\mathcal{E}^{(e)} 表示第ee 个 epoch 边的集合，S(v,v′)S(v,v') 是节点vv 和其邻居节点v′v' 的相似度

  • 定义了两种状态:

    ∙s1⁣:当前epoch的平均节点相似度高于前一个epoch,即G(S)(e−1)<G(S)(e)。∙s2⁣:前epoch的平均节点相似度低于或等于前一个epoch,即G(S)(e−1)≥G(S)(e)。\begin{aligned} \bullet s_{1}\colon\text{当}& \text{前epoch的平均节点相似度高于前一个epoch,即} \\ &G(S)^{(e-1)}<G(S)^{(e)}。 \\ \bullet s_{2}\colon& \text{前epoch的平均节点相似度低于或等于前一个epoch,即} \\ &G(S)^{(e-1)}\geq G(S)^{(e)}。 \end{aligned}

# 动作

  • 强化学习模块的目标是学习最优的邻居过滤阈值 $ p$。

  • 动作空间AA 定义了两个动作:

    • a1a_1: 增加采样概率pp 和一个固定步长τ\tau
    • a2a_2: 减少采样概率pp 和一个固定步长τ\tau

  • 根据当前状态ss，通过映射关系π\pi 选择动作：

    a=π(s)={p+τ,ifs=s2p−τ,ifs=s1a=\pi(s)=\begin{cases}p+\tau,&\text{if} s=s_2\\p-\tau,&\text{if} s=s_1\end{cases}

# 奖励机制

  • 奖励函数f(p,a)(e)f(p,a)^{(e)} 用于评估每个 epoch 的动作效果:

    f(p,a)(e)={+1,ifG(S)(e−1)≤G(S)(e)−1,ifG(S)(e−1)>G(S)(e)f(p,a)^{(e)}=\begin{cases}+1,&\text{if}G(S)^{(e-1)}\leq G(S)^{(e)}\\-1,&\text{if}G(S)^{(e-1)}>G(S)^{(e)}\end{cases}

  • 如果当前 epoch 的平均距离（即相似度的负数）比前一个 epoch 更小（表示相似度更高），则给予正奖励 +1，反之则给予负奖励 -1。

  • 奖励机制确保采样概率 $ p$ 的调整能够逐步收敛到一个最优值，从而在每个节点的邻居中选择最合适的邻居集合。

# 终止条件

  • 终止条件是为了节省计算资源，当模型在最后 15 个 epoch 中收敛时，认为最优阈值p(l)p^{(l)} 已经找到，此时终止强化学习模块。

  • 终止的具体条件是：如果在最后 15 个 epoch 中，奖励函数的和满足以下条件：

    ∣∑e−15ef(p,a)(e)∣≤2\left|\sum_{e-15}^ef(p,a)^{(e)}\right|\leq2

    则认为模型已经收敛并且停止更新

# 敏感学习

邻居采样的影响：在执行邻居采样之后，新生成的图可以显著减少正节点的负邻居节点数量。这样做的目的是减少不相关的或负面的影响，从而提高模型的准确性。

极端情况的风险：尽管减少负邻居节点数量有助于提高模型性能，但如果过度减少，甚至完全平衡图中的正负样本数量，反而会对模型产生不利影响。具体来说，过多的负节点被过滤掉可能导致大量有效数据丢失。这种数据丢失会削弱模型的学习能力，从而降低模型的整体表现

成本敏感学习器的引入：为了应对上述问题，设计了一种成本敏感学习器，用于在邻居采样后训练 GNN 的输出嵌入。该学习器旨在平衡样本不均衡对模型的影响。

# 模块组成

GNN 节点嵌入学习模块：负责从图中学习节点的嵌入表示。

成本敏感模块：在嵌入学习的基础上，结合不同类别的分类成本，调整模型的决策过程，从而提高模型在不均衡数据集上的表现。

# 邻居信息聚合

注意力机制与权重参数：许多现有的 GNN 模型倾向于使用注意力机制或设计加权参数来进行消息聚合，以提高模型的性能。这些方法通过在消息传递和聚合过程中对邻居节点施加不同的权重来优化节点的表示。

计算成本问题：然而，当已经为每个节点选择了最相似的邻居后，使用注意力系数或加权参数在信息聚合中可能意义不大，并且会显著增加计算成本

平均聚合器（Mean Aggregator）：为了在节省计算成本的同时保留领域中的重要信息，作者选择了一种简单且高效的聚合器 ——GraphSAGE 模型中的平均聚合器（Mean Aggregator）。

  • 与注意力机制相比，平均聚合器大大降低了模型的复杂性，同时仍然能够有效地进行信息聚合。

# 具体实现

hv(l)=σ(W⋅AGG({hv(l−1)}∪{hv′(l−1),∀v′∈N(v)}))⋅这里,σ是激活函数,W是需要学习的权重矩阵。⋅N(v)是节点v的邻居节点集合。聚合函数AGG使用的是平均聚合（MEAN），即对节点及其邻居的嵌入进行平均。\begin{aligned} &h_{v}^{(l)}=\sigma\left(\mathbf{W}\cdot\mathrm{AGG}\left(\{h_{v}^{(l-1)}\}\cup\{h_{v^{\prime}}^{(l-1)},\forall v^{\prime}\in\mathcal{N}(v)\}\right)\right) \\ &· 这里,\sigma 是激活函数,W是需要学习的权重矩阵。 \\ &· \mathcal{N}(v)\text{ 是节点 }v\text{ 的邻居节点集合。} \\ &聚合函数 AGG 使用的是平均聚合（MEAN），即对节点及其邻居的嵌入\\ &进行平均。 \end{aligned}

AGG({hv(l−1)}∪{hv′(l−1),∀v′∈N(v)})=1∣N(v)∣+1∑v′∈{v}∪N(v)hv′(l−1)\mathrm{AGG}\left(\{h_v^{(l-1)}\}\cup\{h_{v'}^{(l-1)},\forall v'\in\mathcal{N}(v)\}\right)=\frac{1}{|\mathcal{N}(v)|+1}\sum_{v'\in\{v\}\cup\mathcal{N}(v)}h_{v'}^{(l-1)}

平均操作：MEAN () 函数表示对集合中节点的嵌入取平均值。

下游任务：将节点的嵌入 hv(l)h_v^{(l)} 作为最后一层 GNN 输出的表示，用于执行后续的下游任务（例如节点分类或边预测等）。

# 降低成本的学习方案

不平衡图中的问题：在处理不平衡图时，直接使用节点嵌入进行下游任务（如节点分类）通常效果不佳。为了解决这个问题，作者引入了成本敏感学习。

基本思路：通过对节点嵌入应用成本敏感矩阵 $ C，来调整每个节点，来调整每个节点 v 属于不同类别属于不同类别 k 的概率的概率 p_k (v)$。具体算法如下:

pk(v)=Softmax(C[v,k]⋅zv[k])=Cv,kexp⁡(zv[k])∑k′Cv,k′exp⁡(zv[k′])\begin{aligned} p_{k}(v)& =\mathrm{Softmax}\left(\mathbf{C}[v,k]\cdot\mathbf{z}_{v}[k]\right) \\ &=\frac{\mathbf{C}_{v,k}\exp\left(\mathbf{z}_{v}[k]\right)}{\sum_{k^{\prime}}\mathbf{C}_{v,k^{\prime}}\exp\left(\mathbf{z}_{v}\left[k^{\prime}\right]\right)} \end{aligned}

  • C[v,k]C[v,k] 是成本矩阵CC 中的元素，表示将节点vv 分配到类别kk 的成本
  • zv[k]z_v[k] 是节点vv 的最终嵌入中第kk 维的值

# 成本矩阵的挑战

挑战：主要挑战在于如何合理确定成本矩阵 $ C$ 中每个元素的值。过去的工作通常根据专家经验或数据中的不平衡率来设定这些值，但这种方法不能自适应地应对数据集的变化。

解决方案：为了解决这个问题，作者设计了一种可自动优化的成本敏感矩阵算法。

# 成本矩阵的优化

  1. 数据分布矩阵（H Matrix）：数据分布矩阵 $ H$ 考虑了训练集中不同类别数据的分布情况。对于多数类样本，应该分配较低的成本，而对于少数类样本，应该分配较高的成本。

    数据分布直方图矩阵H(i,j)定义如下:H(i,j)={max⁡(hi,hj),ifi≠j,(i,j)∈Chi,ifi=j,i∈C其中hi表示类别i的直方图分布。\begin{gathered} \text{数据分布直方图矩阵 }H(i,j)\text{ 定义如下:} \\ H(i,j)=\begin{cases}\max(h_i,h_j),&\text{if }i\neq j,(i,j)\in C\\h_i,&\text{if }i=j,i\in C\end{cases} \\ \text{其中 }h_i\text{ 表示类别 }i\text{ 的直方图分布。} \end{gathered}

  2. 散布矩阵（S Matrix）：散布矩阵 $ S $ 用于衡量同类样本的嵌入在高维空间中的聚集程度。样本同类的嵌入应当距离较小，而不同类样本的嵌入应当距离较大。

    ∙类内散布矩阵SW定义为:SW=∑i=1K(1Ni∑j=1Ni(xi,j−mi)(xi,j−mi)⊤)∙类间散布矩阵SB定义为:SB=∑i=1K(mi−m)(mi−m)⊤其中mi是类别i的样本均值,m是所有类别样本的总均值。∙最终的散布矩阵S定义为:S=SWSB\begin{gathered} \bullet\text{ 类内散布矩阵 }S_{W}\text{ 定义为}: \\ S_{W}=\sum_{i=1}^{K}\left(\frac{1}{N_{i}}\sum_{j=1}^{N_{i}}(x_{i,j}-m_{i})(x_{i,j}-m_{i})^{\top}\right) \\ \bullet\text{ 类间散布矩阵 }S_B\text{ 定义为:} \\ S_B=\sum_{i=1}^K(m_i-m)(m_i-m)^\top \\ 其中m_i是类别i的样本均值,m是所有类别样本的总均值。 \\ \bullet\ 最终的散布矩阵S定义为: \\ S=\frac{S_{W}}{S_{B}} \end{gathered}

  3. 归一化混淆矩阵（R Matrix）：归一化混淆矩阵 $ R$ 用于捕捉分类结果中的误分类信息。当前 epoch 中误分类的样本应在下一 epoch 中获得更大的权重。

    R(i,j)=∣{v∣argmaxkpk(v)=j,yv=i}∣∣V∣\mathbf{R}(i,j)=\frac{\left|\left\{v\mid\underset{k}{\text{argmax}}p_k(v)=j,y_v=i\right\}\right|}{|\mathcal{V}|}

    # 最终优化目标

    将上述三种矩阵 $ H、S、R 结合起来，定义了一个成本矩阵的优化目标结合起来，定义了一个成本矩阵的优化目标 T$:

    T=β⋅H∘S∘R其中β是超参数,∘表示Hadamard乘积(元素乘积)。T=\beta\cdot H\circ S\circ R\\\text{其中 }\beta\text{ 是超参数,}\circ\text{表示Hadamard乘积(元素乘积)。}

    最终的成本函数Lcost(C,T)用于衡量训练成本矩阵C与目标T之间的差异:Lcost(C,T)=∣∣T−C∣∣22+Eval(θ,C)其中Eval是验证误差。\begin{aligned} &最终的成本函数~L_{cost}(C,T)~用于衡量训练成本矩阵~C~与目标~T~之间的\text{差异:} \\ &L_{cost}(C,T)=||T-C||_{2}^{2}+E_{val}(\theta,C) \\ &\text{其中 }E_{val}\text{ 是验证误差。} \end{aligned}

# 成本敏感学习初始化

初始化方法的局限性：传统的神经网络权重初始化方法，如 Xavier 初始化、Kaiming 初始化和随机初始化，通常适用于神经网络的大量参数。然而，这些方法在成本敏感矩阵 $C 上的应用效果不佳，因为上的应用效果不佳，因为 C 的维度通常很小（的维度通常很小（K \times K$），无法展示随机初始化的有效性。此外，这些方法也无法捕捉成本敏感学习的目标，即在模型中对少数类样本施加正确的成本影响。

# 从不平衡率IRIR 出发

为了克服上述问题，作者提出了基于样本不平衡率（IR）的初始值设定方法。具体地，考虑到 IR 的反比，使用其对数变换来初始化成本矩阵 $ C$ 中的每个元素：

Cij=log⁡(1IR)=log⁡(∣Cj∣∣Ci∣+1)其中,∣Ci∣和∣Cj∣分别表示类别i和类别j的样本数量。这种方法能够将有偏的成本值转换为一个无偏的正态分布。\begin{aligned} &C_{ij}=\log\left({\frac{1}{\mathrm{IR}}}\right)=\log\left({\frac{|C_{j}|}{|C_{i}|}}+1\right) \\ &\text{其中,}|C_i|\text{ 和 }|C_j|\text{ 分别表示类别 }i\text{ 和类别 }j\text{ 的样本数量。这种方法能够将有} \\ &\text{偏的成本值转换为一个无偏的正态分布。} \end{aligned}

# 成本矩阵优化

优化目标：在初始化成本矩阵后，作者定义了一个成本函数Lcost(C,T)L_{cost}(C, T)，并在每个 epoch 中通过一定的学习速率对成本矩阵 $ C$ 进行优化。优化目标是找到一个最优的成本矩阵 C∗C^*，使得：

C∗=arg⁡min⁡CLcost(C,T)C^*=\arg\min_CL_{cost}(C,T)

梯度下降法：为了解决上述优化问题，作者使用了梯度下降（Gradient Descent, GD）算法来计算每一步的更新方向。具体计算公式如下：

∇Lcost(C,T)=∇(va−vb)(va−vb)T=(va−vb)JvbT=−(va−vb)1T\begin{gathered} \nabla\mathcal{L}_{\mathrm{cost}}(\mathbf{C},\mathbf{T}) =\nabla\left(\mathbf{v}_{a}-\mathbf{v}_{b}\right)\left(\mathbf{v}_{a}-\mathbf{v}_{b}\right)^{T} \\ =(\mathbf{v}_{a}-\mathbf{v}_{b}) \mathbf{J}_{\mathbf{v}_{b}}^{T} \\ =-\left(\mathbf{v}_{a}-\mathbf{v}_{b}\right)\mathbf{1}^{T} \end{gathered}

其中，va\mathbf{v}_a 和 $ \mathbf {v}_b$ 是成本矩阵 $ C 和目标矩阵和目标矩阵 T的向量化表示，的向量化表示，\mathbf {J}$ 是 Jacobi 矩阵。

image.png

# 成本敏感图神经网络算法及流程

# 算法损失函数定义

  • GNN 的交叉熵损失（CE loss）：
    在给定的欺诈检测图 $ G和节点集合和节点集合 V_{\text {train}}$ 的情况下，GNN 的交叉熵损失函数定义为：

    LGNN=−∑v∈Vyvlog⁡(pv)L_{\mathrm{GNN}}=-\sum_{v\in\mathcal{V}}y_v\log(p_v)

    其中yvy_v 是节点 $ v的真实标签，的真实标签，p_v是节点是节点 v$ 的预测概率。

  • CSGNN 的损失函数:
    CSGNN 的总损失函数结合了 GNN 的交叉熵损失和节点特征变换的损失函数：

    LCSGNN=LGNN+λLtransLtrans=−∑v∈Vyvlog⁡(hv)L_{CSGNN}=L_{GNN}+\lambda L_{trans}\\\mathcal{L}_{trans}=-\sum_{v\in V}\mathbf{y}_v\log\left(\mathbf{h}_v\right)

# 算法流程

image.png
算法的整体流程如下：

image.png

# 输入：

  • 一个无向图，其中包含节点特征和标签，记为G=(V,X,A,E,Y)G = (\mathcal{V}, \mathcal{X}, \mathcal{A}, \mathcal{E}, \mathcal{Y})
  • 节点类别的数量KK。
  • 图神经网络的层数 $ L 和训练周期数和训练周期数 E$。

# 输出：

  • 节点v∈Vtrainv \in V_{\text{train}} 的向量表示 pvp_v。

# 初始化：

  1. 根据公式Cij=log⁡1p(1IR)=log⁡(∣Cj∣∣Ci∣+1)\mathbf{C}_{ij}=\log1p\left(\frac{1}{IR}\right)=\log\left(\frac{|C_j|}{|C_i|}+1\right)，为训练集VtrainV_{\text{train}} 中的所有节点初始化成本矩阵 C_

# 模块训练：

  1. 特征变换：

    • 使用公式（hv=σ(Wxv)h_v=\sigma(Wx_v)）进行节点特征变换，生成节点嵌入h_v^
    • 计算节点特征变换的损失LtransL_{\text{trans}}（Ltrans=−∑v∈Vyvlog⁡(hv)\mathcal{L}_{trans}=-\sum_{v\in V}\mathbf{y}_{v}\log\left(\mathbf{h}_{v}\right)）。

  2. 基于强化学习的邻居采样：

    • 进入循环，直到满足某个停止条件：
      • 计算节点 $ v的相似度得分的相似度得分 S (v, v')和图的相似度度量和图的相似度度量 G (S)$。
      • 使用奖励函数f(p,a)(e)f(p, a)^{(e)} 更新采样概率 $ p$。
      • 这个步骤是为了通过强化学习选择最合适的邻居节点进行聚合。

  3. 图神经网络（GNN）：

    • 对于每一层 $ l$:

      • 计算当前层的节点嵌入hv(l)h_v^{(l)}。

    • 生成节点的输出嵌入zv(L)z_v^{(L)}，并根据公式（1313）计算节点的分类概率 pv(k)p_v(k)

      公式(13)pk(v)=Softmax(C[v,k]⋅zv[k])=Cv,kexp⁡(zv[k])∑k′Cv,k′exp⁡(zv[k′])\begin{aligned} &公式(13)\\ p_{k}(v)& =\mathrm{Softmax}\left(\mathbf{C}[v,k]\cdot\mathbf{z}_{v}[k]\right) \\ &=\frac{\mathbf{C}_{v,k}\exp\left(\mathbf{z}_{v}[k]\right)}{\sum_{k^{\prime}}\mathbf{C}_{v,k^{\prime}}\exp\left(\mathbf{z}_{v}\left[k^{\prime}\right]\right)} \end{aligned}

  4. 更新损失：

    • 计算 GNN 的交叉熵损失 LGNNL_{\text{GNN}}
    • 计算数据分布矩阵 $ H、散布矩阵、散布矩阵 S 和混淆矩阵和混淆矩阵 R$
    • 计算成本矩阵的目标TT，并根据公式（20）优化成本损失LcostL_{\text{cost}}
    • 最终，结合所有损失，得到 CSGNN 的总损失LCSGNNL_{\text{CSGNN}}